Um caminhão de massa desce uma ladeira que faz uma inclinação angular com a horizontal a uma velocidade constante . O caminhão carrega na carroceria uma caixa de massa . Ao avistar um obstáculo na pista, o motorista freia bruscamente, travando os pneus, e começa a derrapar. O coeficiente de atrito cinético entre as rodas do caminhão e o chão é , e o coeficiente estático entre a caixa e o caminhão é tal que o objeto não desliza.
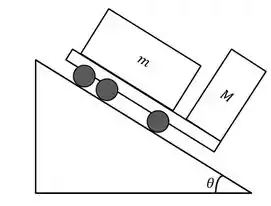
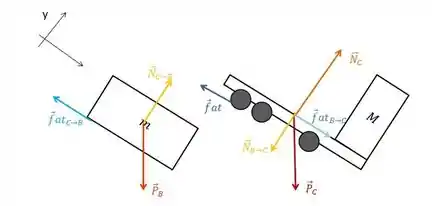
(a) Desenhe na figura todas as forças exercidas no caminhão e na caixa.
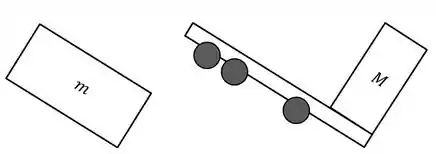
(b) Quais são os pares de força de ação e reação?
(c) Calcule a força de atrito exercida no caminhão e na caixa como função das variáveis do problema.
(d) Qual o limite das forças de atrito para e
(e) Substituindo os valores de , e encontre a distância percorrida até o caminhão parar. Utilize e aproximação e .
(f) O que você deverá mudar em seus cálculos se o caminhão estiver subindo a ladeira em vez de descendo? Recalcule o resultado do ítem anterior para este caso.
Passo 1
(a)
Vamos lá. A questão ta pedindo pra gente desenhar as forças na caixa que o caminhão tá carregando e no caminhão.
Bom, ambos estão sobre atração gravitacional, então temos o peso, além disso, ambos estão sobre uma superfície, então têm a normal. O bloco sofre uma força de atrito exercida pela superfície do caminhão, que é o que permite a ele ficar parado. O caminhão sofre atrito com o chão, e além disso, ele é a superfície para o bloco, então como o bloco “sente” a normal e a força de atrito, que são forças de superfície, o caminhão vai sentir a reação a essas forças.
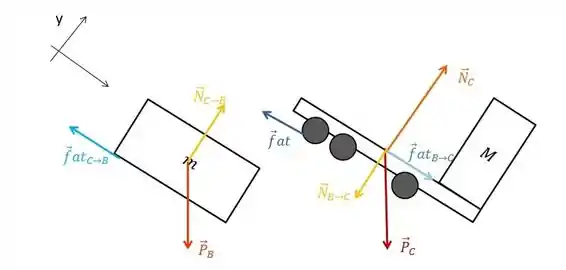
Para o bloco:
é o peso do bloco, é a força de atrito que o bloco sofre pela superfície, que é a caçamba do caminhão e é a normal que o bloco sente pela superfície, que nesse caso, também é a caçamba do caminhão.
Para o caminhão:
é o peso do caminhão, é a força de atrito que o caminhão sofre pela superfície, que é o chão e é a normal que o caminhão sente pela superfície que é o chão. é uma força de reação ao contato entre bloco/caminhão. Da mesma forma, é a força que o bloco faz na superfície.
Show?!
Passo 2
(b) Quais são os pares de força de ação e reação?
A gente até já falou ali em cima, se o bloco faz força na superfície (caminhão) então o caminhão faz força no bloco.
São elas:
e
e
Portanto já podemos dizer que, os módulos delas são iguais, pela terceira lei de Newton, e só o sentido são diferentes:
Passo 3
(c)
Pra gente calcular a força de atrito no caminhão, que é causada pelo chão, , e a força de atrito no bloco, que é causada pelo caminhão, , temos que aplicar a segunda lei de Newton em cada corpo.
Vamos usar o diagrama de forças da letra a e o sistema de coordendas que desenhamos, já marquei o ângulo de inclinação do plano ali, que é pra ficar mais fácil na hora de decompor as forças:
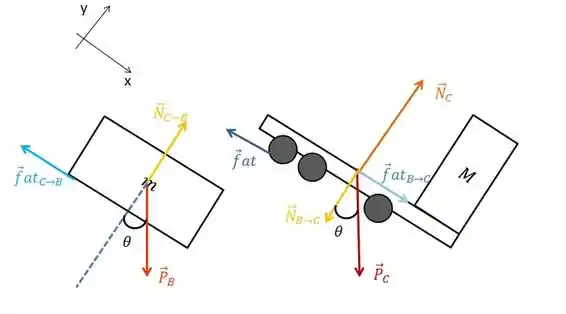
Para o bloco:
Na direção do eixo y (a aceleração em y é zero, já que não há movimento nessa direção):
Decompondo as forças nessa direção:
Já podemos ajeitar:
Beleza, na direção do eixo x (o bloquinho tá parado em relação ao caminhão, mas ele tá se movendo junto com o caminhão então, nessa direção ambos possuem a mesma aceleração):
Show? Guarda essas duas equações aí porque já vamos precisar delas de novo.
Vamos aplicar a segunda lei para o caminhão agora:
Na direção y, também não temos aceleração, mesmo caso do bloco):
Para o eixo x, temos a mesma aceleração do bloquinho:
Beleza, vamos usar a relação que vimos na letra b, dos pares ação e reação:
Substituindo essas relações nas equações do caminhão:
Beleza?
Opa!!! Aqui a gente já consegue saber a entre o caminhão e o chão. Se liga só:
Sabemos que
E pela equação ali em cima:
Pegando o lá da equação para o corpo:
Temos que:
Então:
Maravilha!!! Uma já foi...mas falta ainda a entre o bloco e o caminhão.
Passo 4
Vamos usar as equações do bloco para isolar a aceleração, e depois brincar de substituir nas equações de movimento para acharmos a forças de atrito :
Então:
Maravilha, agora substituindo isso na equação do caminhão:
Já sabemos a que é:
Substituindo isso:
Ajeitando essa equação e isolando :
Uhuuul! Finalmente!!
Vamos pra próxima agora!!
Passo 5
(d) Qual o limite das forças de atrito para e
Aí é só a gente ver quanto a fat vale nesses casos.
Entre o caminhão e o chão:
Para , significa que estamos em um plano reto...não tem inclinação:
Para , significa que o plano tá completamente vertical...eita..Como que o caminhão vai subir? Ele não vai né! Ele vai cair, ou seja, não vai ter contato dele com o chão, logo:
Entre o bloco e o caminhão:
Para
Para
Maravilha! Essa foi tranquila! Vamos pra próxima.
Passo 6
e)
Ele fala pra gente que , e , e pede pra gente calcular a distância até o caminhão parar.
Beleza, a gente sabe a aceleração que ele tem, sabemos a velocidade final, que é zero, e a inicial que é 15 m/s. Então vamos usar Torricelli:
Pegando a aceleração de descobrimos lá na letra c:
E substituindo tudo:
A gente descobriu a força de atrito na letra anterior:
Então substituindo na equação acima, e arrumando:
Substituindo os valores que ele fala pra gente:
Então:
Passo 7
f) Bem, se o camihão estivesse subindo a ladeira, então o movimento dele seria no sentido oposto ao do eixo x, que desenhamos lá na nossa figura, então a nossa aceleração, teria sentido oposto:
Vamos ver como isso muda as coisas:
Substituindo tudo e arrumando:
Então:
Agora o deslocamento é negativo. Como era de se esperar, já que ele tá indo no sentido oposto ao do eixo x, que tínhamos definido.
Só sucesso?!
Resposta
a)
b) e
e
c)
d)Entre o caminhão e o chão:
Para
Para
Entre o bloco e o caminhão:
Para
Para
e)
f)