Dois blocos de massa e estão ligados por um fio ideal como ilustrado na figura abaixo.
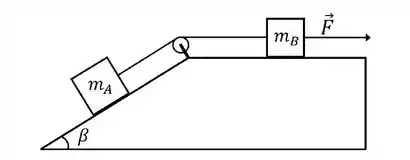
O bloco de massa desliza sobre a parte inclinada de um ângulo em relação à horizontal. Já o bloco de massa desliza sobre uma superfície plana. Sobre o bloco atua uma força de módulo paralela à horizontal. O coeficiente de atrito cinético entre os blocos e a superfície é igual .
Considerando que devido à ação da força o sistema passa a se mover para a direita:
a) Desenhe o diagrama de forças para cada um dos blocos.
b) Determine a aceleração do conjunto.
c) Determine a tensão no fio que une os blocos.
Suas respostas devem ser dadas em termos de ,, , , e .
Passo 1
a) Desenhe o diagrama de forças para cada um dos blocos.
Vamos lá!!
Os dois blocos vão ter peso, normal, tração e força de atrito. E além dessas, o bloco B tem a força F.
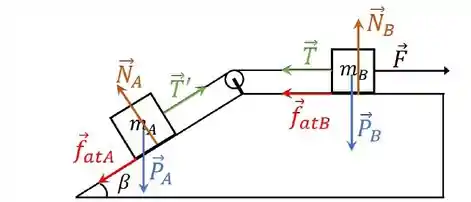
Uma coisa legal pra notar é que, como o fio e a roldana são ideais, vamos ter que o módulo das trações são iguais:
Show?
Passo 2
b) Determine a aceleração do conjunto.
Vamos aplicar a segunda lei de newton em cada um dos blocos.
Primeiro para o bloco A:
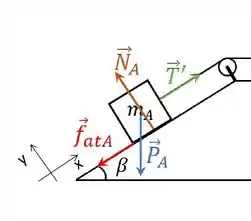
Usando esse sistema de coordenadas da figura, vamos ter:
Em x:
Em y, não tem movimento, então:
Opa!
A gente sabe que:
Substituindo:
Então a equação lá de cima fica:
Beleza. Guarda essa equação aí. Daqui a pouco vamos precisar dela.
Agora, vamos fazer a mesma coisa, mas para o bloco B.
Passo 3
Para o bloco B
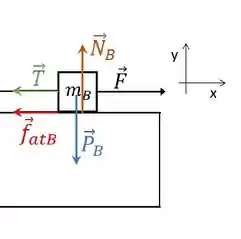
Usando esse sistema de coordenadas da figura, vamos ter:
Em x:
Em y, não tem movimento, então:
Mesma coisa de antes:
Substituindo na equação lá de cima:
Show!! Tá bonito...
Agora, lembra que a gente falou que o módulo das trações são iguais, então:
Aí, olha só pra essas 2 equações que a gente achou:
Elas vão ficar assim:
Pra gente achar a aceleração é só resolver esse sisteminha.
Vamos somar as equações e isolar o :
Uhuuul!!!
É esse negócio gigante mesmo!
Hahah
Passo 4
c) Determine a tensão no fio que une os blocos.
Agora é tranquilo... lembra daquelas equações que a gente achou na letra b:
Aí é só substituir o em qualquer uma delas, e isolar o
Vamos pegar a segunda:
Arrumando isso:

Resposta
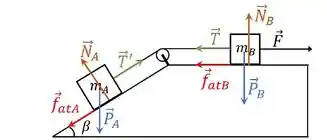 a)
a)
b)
c)