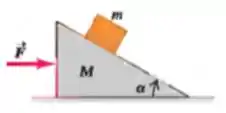
Um cunha de peso e ângulo está sobre uma superfície horizontal sem atrito. Um bloco de peso é posto sobre a cunha e uma força horizontal é aplicada na cunha (veja a figura). Também não há atrito entre o bloco e a cunha. Qual deve ser o módulo de se queremos que o bloco permaneça a uma altura constante acima da superfície horizontal?
Passo 1
Antes de tudo, diagrama das forças no sistema.
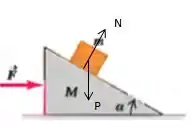
Passo 2
Normalmente, a gente decompõe as forças na direção paralela e perpendicular à rampa...
PORÉM, nesse caso queremos descobrir uma força que atua na horizontal, para isso, precisamos descobrir a aceleração do bloco na direção dessa força (horizontal).
Então, diferente do que estamos acostumados para um plano inclinado, vamos decompor as forças nos eixos padrões, (horizontal) e (vertical):
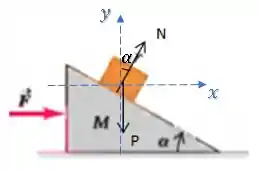
Assumindo que o corpo não se mexe verticalmente, no eixo temos:
E no eixo :
Se dividirmos uma equação pela outra vamos ter
Como
Ou seja, o módulo da aceleração correspondente à força é igual à aceleração da gravidade.
Passo 3
Olhando para o sistema, a força resultante sobre o plano e o bloco é
Como já sabemos
Os dois termos na direita são os pesos do bloco e do plano que foram dados no enunciado, assim