Parte I:
Uma caixa de massa está sobre um plano inclinado que faz um ângulo com a horizontal. Ela está ligada por uma corda de massa desprezível, que passa por uma roldana ideal, a uma outra caixa de massa , conforme a figura ao lado. Os planos inclinados fazem entre si e não possuem atrito.
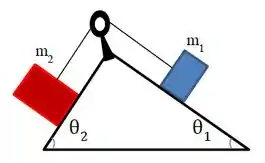
(a ) Faça os diagramas de forças dos blocos 1 e 2.
(b) Determine o módulo da aceleração de cada bloco.
(c) Encontre o módulo da tensão 𝑇 na corda.
Passo 1
Parte I:
Temos dois blocos (1 e 2) em planos inclinados de inclinações diferentes ( e ) conectados por uma corda. A força peso vai puxar cada bloquinho para baixo, e eles vão ficar como se fosse um cabo de guerra:

Se as inclinações fosse iguais, o bloco de maior massa iria ganhar o “cabo de guerra’’, conseguindo descer e puxar o outro bloquinho para cima, pois sua força peso é maior.
Mas como as inclinações são diferentes, o bloco que vai descer será o do lado com uma componente da força peso maior atuando na direção de descida da rampa.
Então, assim como o item (a) já pede, vamos analisar cada bloquinho.
Passo 2
(a) Faça os diagramas de forças dos blocos 1 e 2.
Tanto o bloco 1 quanto o bloco 2, terão força peso () apontando para baixo, força de tração () no sentido da corda e força normal () perpedndicular à superfície de contato.
Bloco 1:
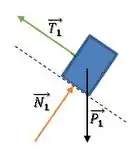
Bloco 2:
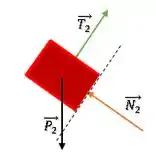
Passo 3
(b) Determine o módulo da aceleração de cada bloco.
Para relacionar os dois blocos, vamos usar que a tração () na corda é a mesma, então os módulos:
Para achar a aceleração de cada bloco, vamos decompor as forças no sistema de eixos na direção da aceleração.
Para o bloco 1:
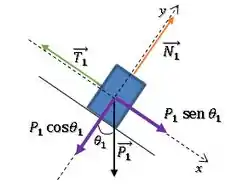
Pela segunda lei de Newton, no eixo temos:
No eixo , vamos assumir que o bloco 1 está descendo (um palpite):
Para o bloco 2:
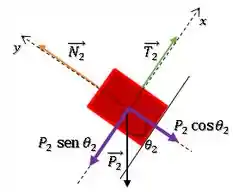
Pela segunda lei de Newton, no eixo temos:
Agora, se consideramos o bloco 1 descendo, o bloco 2 vai estar subindo. Logo, no eixo temos:
Agora vamos somar as equações do eixo de cada bloco:
Temos que :
Não sabemos o ângulo , mas sabemos que e que a rampa é um triângulo retângulo. Logo, . Substituindo nossos dados:
Conseguimos então o módulo da aceleração. Porém, dá uma olhada nessa aceleração negativa. Isso significa que a direção da aceleração está para o lado oposto que consideramos no nosso palpite.
Então, na veradade o bloco 2 está ganhando o “cabo de guerra” e está descendo, enquanto o bloco 1 está subindo. Ambos com aceleração de módulo:
Passo 4
(c ) Encontre o módulo da tensão 𝑇 na corda.
Para achar a tração na corda, vamos usar a equação obtida com a segunda lei de Newton em qualquer um dos blocos, já que a corda tem a mesma tração em todos os pontos.
Vamos escolher o bloco 1:
Antes de substituir. Lembra que no nosso palpite, a aceleração estava no sentido errado do que o sentido que achamos?
Então, devemos manter o sinal negativo da aceleração, pois dessa forma, a equação que achamos fica condizente com o nosso referencial.
Resposta
(a)
Bloco 1:
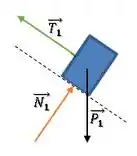
Bloco 2:
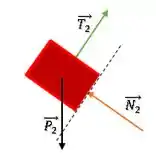
(b)
(c)