Questão 14) Seja a calota esférica dada pela equação , onde . Sobre fixe a orientação tal que . Calcule
Onde
Passo 1
Bem, vamos com calma aqui. Queremos calcular:
Em cima de que nos representa uma “calota”:
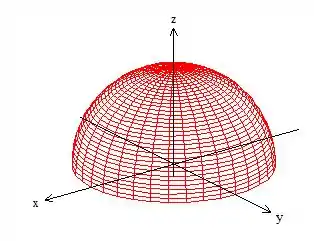
Veja que a calota é uma na realidade a parte de cima da esfera de raio .
Essa integral de superfície é típica de problema de Stokes e é justamente ele que vamos tentar utilizar aqui, já que de acordo com esse Teorema, podemos aplicar
Onde essa integral de linha é calculada na borda de , ou seja, em cima dessa curvinha azul aí:
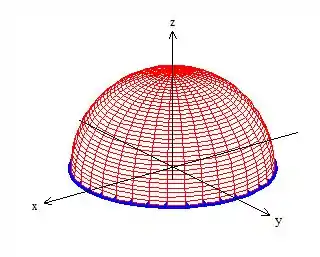
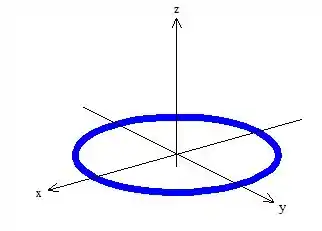
Não sei você, mas eu não quero calcular a integral de linha em cima dessa circunferência aí não! Ora, vai dar mais trabalho! Então o que acha de tentar voltar pra integral de superfície?
Passo 2
Sim, vamos retornar a integral de superfície, mas não pra aquela dali em :
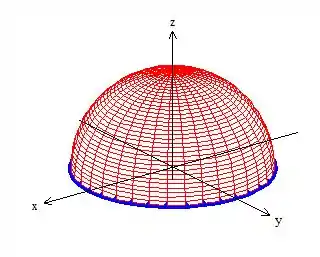
O teorema de Stokes é legal com a gente. Ele fala que se pode calcular a integral de superfície em qualquer superfície desde que a superfície escolhida tenha como borda a curva que eu te mostrei. Ora, e qual superfície, além de , que tem como borda esse cara? O próprio círculo em cima do plano ! :D
Então, chamando esse plano de superfície , , pelo teorema de Stokes...
Logo...
Veja que ironia nessa última igualdade. Nós queríamos calcular uma integral de superfície em cima de uma superfície que não continha o círculo, mas por Stokes calcular a integral em cima dessa calota é o mesmo que calcular em cima do círculo!
Doideira, neh? Então bora comigo calcular essa integral em :D
Passo 3
Primeiro quem é o rotacional?
Como
Então, pelo cálculo das derivadas parciais...
Logo, vamos ter que calcular a integral de superfície desse vetor aí! Fique atento para não esquecer e usar , heim!
Passo 4
Tá, agora quem é a superfície ? Ora é o círculo no plano , neh:
Veja que esse plano tem o vetorsinho normal apontando justamente pra cima, logo ele tem coordenadas:
Esse vetor é justamente o vetor pedido no problema, já que ele aponta pra cima, logo...
Passo 5
Precisamos da superfície parametrizado para prosseguir com os cálculos:
Como é um círculo, podemos parametrizar utilizando coordenadas cilíndricas...
Como o do círculo é conhecido (ele está em cima do plano )...
Então a gente pode em uma notação mais elegante, falar que a parametrização é...
Onde e varia com o círculo. podemos afirmar de antemão que ele dá uma volta completa, logo...
Já o raio, depende do raio do círculo. Bem, podemos encontra esse raio fazendo o na equação da esfera...
Ou seja, é um círculo de raio , logo, o raio varia de até esse cara, veja...
Passo 6
O termo dessa parametrização é...
Onde
Logo...
Passo 7
Voltando para a integral que precisamos resolver...
Colocando esse em coordenadas cilíndricas...
Agora trocando o pelas variações de e enquanto que o ...
Agora é só resolver essa integral e correr para o abraço 😉!
Passo 8
Passo 9
Veja bem, encontramos o valor da integral em . Mas como vimos...
Então
Resposta
Exercícios de Livros Relacionados
Ver Mais
Ver Mais
Ver Mais
Ver Mais
Ver Mais