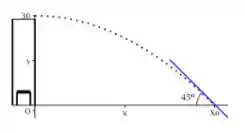
Um aluno foi desafiado a chutar uma bola do alto de um prédio com de altura, de modo a atingir o solo com a inclinação de . Sabendo-se que a bola descreve uma trajetória parabólica dada pela equação , onde é a distância percorrida horizontalmente pela bola, é a altura da bola e é a velocidade horizontal aplicada pelo aluno no momento do lançamento, determine o valor de para que o aluno vença o desafio.
Passo 1
Quando a bola atinge o chão sua altura é , então vamos fazer essa substituição na equação da trajetória para descobrir , que é a distância percorrida, em função da velocidade inicial.
Passo 2
Agora vamos derivar para determinarmos o coeficiente angular da reta tangente à trajetória parabólica no ponto onde a bola toca o chão. Lembre-se que é a velocidade inicial, logo é um valor constante.
Agora podemos achar o coeficiente angular no ponto onde a bola toca o chão, isto é, quando .
Passo 3
A bola deve atingir o solo numa inclinação de negativos (conforme a figura). A inclinação corresponde a tangente do ângulo. A inclinação equivale ao coeficiente angular da reta tangente, portanto: