Um funil cônico têm diâmetro de na parte superior e altura de . Se o funil for alimentado à taxa de e tem uma vazão de , determine quão rapidamente está subindo o nível de água quando esse nível for de .
Passo 1
E ai, xuxus!! Quais as novidades? A que eu tenho pra vocês é que vão tirar 10 nessa matéria :)
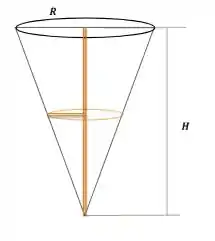
Bom, nossa questão é sobre um funil cônico que é alimentado por água a uma taxa de e a saída desta substância ocorre de acordo com a vazão de . Sendo assim, a questão deseja saber qual será a taxa de variação do nível de água quando a altura correspondente for de . Além disso, a questão nos fornece que o diâmetro da parte superior do funil é de e que a altura total do funil é de . Como proceder???
Passo 2
Primeiro, vamos pensar sobre a variação do volume em relação ao tempo dentro do funil cônico. Temos que a água está entrando a uma taxa e que a saída dessa água ocorre a uma taxa . Portanto, a taxa correspondente ao volume de água que permanece dentro do funil será de:
=
Lembrando que
Assim,
Dessa forma nossa equação correspondente será :
Passo 3
Beleza, mas agora precisamos relacionar isso com o volume do nosso cone.
O volume de um cone é dado pela equação:
E sabemos que o diâmetro da parte superior do nosso cone possui , ou seja,
E além disso, a altura total é de . Vamos supôr que eu irei fatiar esse meu cone em seções paralelas a base do funil, ao fazer isso é possível relacionar o raio de cada seção em relação a altura em que se encontra essa seção, como na figura:
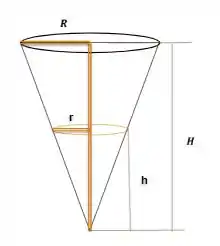
Desse modo, temos que:
Passo 4
Agora que conseguimos relacionar o raio de cada seção com sua altura correspondente, vamos aplicar esse valor na fórmula do volume de um cone.
O volume de um cone é dado pela equação:
Utilizando , temos que :
Aplicando a derivada do volume em relação a altura, temos:
Passo 5
Como estamos interessados na variação do nível da água em relação ao tempo e até agora possuímos apenas a derivada do volume em relação a altura, manipularemos a nossa equação de modo que se obtenha a variação desejada:
No passo 2, obtemos que , logo:
Agora encontramos a variação do nível da água em relação ao tempo, só falta encontrar para . Basta substituir esse valor na nossa equação:
E aí? Essa resolução te ajudou? Responde aí!
:)
Resposta
eg