Um carro, vindo do norte, aproxima-se de um cruzamento em ângulo reto a uma velocidade de . Ao mesmo tempo, um outro carro, que se situa à leste do cruzamento, afasta-se a uma velocidade de . Determine a taxa de variação da distância entre os dois carros no instante em que o primeiro está a do cruzamento e o segundo está a do cruzamento. Qual a interpretação física do sinal do resultado encontrado?
Passo 1
E aii, galerinha!! Como estão? Vamos juntos pra mais uma!!
A melhor forma de começarmos a nossa questão é visualizar a situação em questão. Os carros estão se cruzando assim como a figura abaixo:
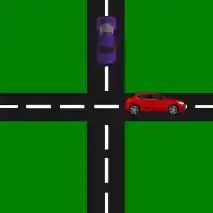
Uma boa forma de modelar o nosso problema é pensar em um triângulo, uma vez que se está interessado na variação da distância entre os automóveis. Além do fato de que o ângulo entre os automóveis é de 90°. Portanto a distância entre os automóveis vai ser dada por .
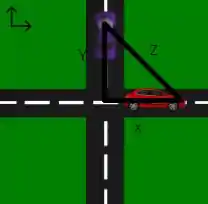
Passo 2
Bom, podemos começar pensando nas equações do espaço em função do tempo para cada carro.
O enunciado nos diz que o carro roxo possui a velocidade constante de , como a trajetória é retilínea logo temos que :
E para o carro vermelho o enunciado afirmou que sua velocidade constante era de :
Passo 3
Como já esboçamos a distância entre os carros (, devemos então encontrar a taxa de variação dessa distância, ou seja, devemos encontrar a derivada de em relação ao tempo.
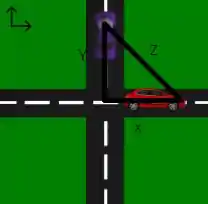
Por formar um triângulo retângulo aplicamos o Teorema de Pitágoras:
E como estamos interessados na derivada de , aplicaremos a derivada em toda a expressão.
Como são funções de aplicaremos a regra da cadeia:
E sabemos que
Assim,
Logo:
Passo 4
Como já sabemos as funções das posições então podemos calcular suas derivadas:
Logo,
Tranquilo??
Bora aplicar na fórmula então!
Passo 5
A questão nos informou também que em um dado tempo :
Portanto,
Como o sinal da taxa de variação da distância é negativa significa que os automóveis estão se aproximando.

E aí, fofuchos!!! Te ajudei?!
Bons Estudos! :)
Resposta
, indica que os automóveis estão se aproximando