Uma partícula se move sobre a elipse ( e medidos em metros) deslocando-se no sentido anti-horário. No instante em que ela passa pelo ponto , sua coordenada decresce a uma taxa de . Quão rápido está variando a distância da partícula à origem nesse instante ?
Passo 1
Um bom primeiro passo pra gente não enrolar a cabeça é esboçar a situação. Vamos então esboçar:
- Uma elipse
- O ponto
- Indicação do sentido antihorário.
- Distância ponto-origem
Olha só como fica:
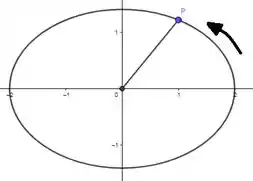
A questão está pedindo a taxa de variação da reta desenhada na figura acima! Como ela pode ser encontrada por Pitágoras da seguinte forma:
Então pra saber a taxa de variação em relação ao tempo, basta a gente derivar , beleza? Pra ficar mais tranquilo de escrever, vamos usar o pra representar essa derivada em relação ao tempo:
O que é o mesmo que:
Passo 2
Olha só galera, a gente não sabe exatamente qual o instante , mas como tanto são funções desse instante, podemos considerar:
Como sabemos as coordenadas no instante , então parte do problema ta dado! O enunciado é bonzinho e ajuda a gente. Saca só:
Sabemos ainda o valor de ! Afinal, essa é a taxa de variação no tempo da coordenada . Como o enunciado também da pra gente isso, nossa expressão de então ganha uma nova cara:
O que por fim, dá:
Vai faltar só a gente achar ! E é isso que vamos fazer no próximo passo, então borá lá!
Passo 3
Beleza, pra achar é tranquilo se lembrarmos da equação da elipse. Dá uma olhada:
Po, é só derivar implicitamente em relação ao tempo que o aparece! Fazendo isso então:
E a gente sabe tudo aí! Substituindo:
Ficamos com:
Passo 4
E fechou, agora é só a gente juntar tudo:
A gente parte pro abraço então depois de juntar e ajeitar esse resultado!
O que, por fim, dá: