Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Stokes

Ver Teoria
Exercício 123123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere as superfícies

S : z = x - 1 2 + y 2 z ≤ - 2 x + 2                                                                                     S - : z = - 2 x + 2 x - 1 2 + y 2 ≤ z

E seja F : R 3 → R 2 o campo de vetores dado por F x ,   y ,   z = 2 x - y + 2 z ,   e 2 x + z - 2 ,   e z 2 + y .

  1. Faça em um mesmo desenho um esboço das superfícies S e S - .
  2. Calcule a área da superfície S - .
  3. Calcule o rotacional do campo F .
  4. Seja γ o bordo de S , orientado de tal forma que sua projeção no plano x y esteja orientada no sentido anti-horário. Calcule ∫ γ   F d s .

Dica: use o Teorema de Stokes, trocando a superfície S por S - . A integral vai estar relacionada com o item 2.b

Passo 1

Letra a) para a gente começar esse problema, vamos começar entendendo quem são essas duas equações que compões essas superfícies.

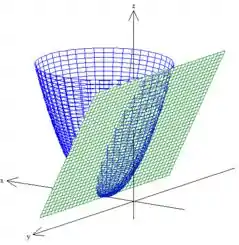
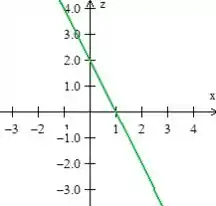
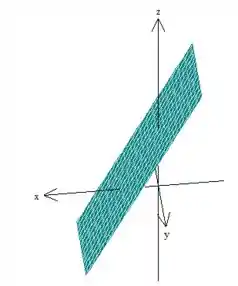
Então, aqui a gente nota que temos uma superfície bem familiar: z = - 2 x + 2 . Essa equação representa pra gente um plano paralelo ao eixo y (pois não tem y nela). Para desenhar esse plano, basta desenhar essa reta no plano z x em seguida deslocar essa reta, dessa forma:

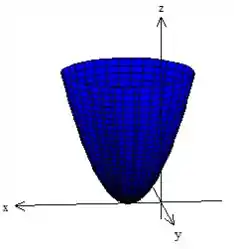
Beleza, mas e essa outra equação aqui: z = x - 1 2 + y 2 ? Cara, essa equação aí nos representa um paraboloide!:) Mas calma que não é um paraboloide qualquer. Esse paraboloide aí está deslocado uma unidade no eixo x , dessa forma aqui:

Passo 2

Beleza! Conhecemos as duas componentes das superfícies S   e   S - , agora quem são essas superfícies mesmo?

Pow, quanto a superfície S , estamos falando de uma superfície em cima do paraboloide, pois z = x - 1 2 + y 2 , mas só queremos a parte que está abaixo do plano verde.

A superfície S - está em cima do plano. Porém, como tem esse sinal de menor ou igual aqui: x - 1 2 + y 2 ≤ z ; isso apenas nos diz que queremos o pedacinho do plano dentro do paraboloide.

Logo, essas duas coisas juntas ficará:

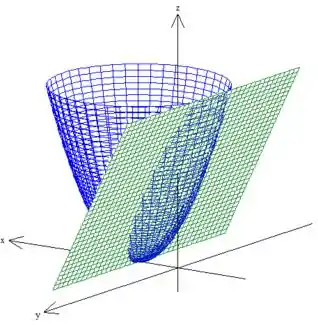
Onde S é a parte de baixo do azul enquanto S - é a parte em cima do plano verde dentro do paraboloide.

Passo 3

Letra b) Para calcular a área de uma superfície vamos utilizar a ajuda de uma integral de superfície:

Á r e a S - = ∬ S -   1 d S

Já vimos que, antes de tudo, deve-se parametrizara a superfície dada. Como estamos trabalhando com uma superfície em cima de um plano, é interessante a gente parametrizar como uma função explícita:

x = u

y = v

z = - 2 u + 2

Mas onde u e v variam?

Passo 4

Para determinar os limites, vamos olhar para a projeção da superfície S - no plano x y , ou seja, vamos olhar de cima para baixo no desenho do passo 2:

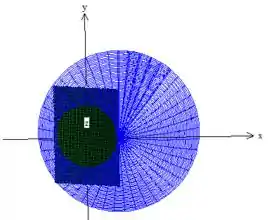
Como podemos perceber, o plano está em intersecção com o paraboloide azul. Logo, a variação das variáveis u e v está dento dessa intersecção (nesse círculo verde). Agora, quem é esse círculo? Pra isso, basta substituir as novas variáveis na inequação que delimita S - :

z = - 2 u + 2 x - 1 2 + y 2 ≤ z     ⇒                         u - 1 2 + v 2 ≤ - 2 u + 2

Resolvendo esse quadrado do primeiro lado da equação...

u 2 - 2 u + 1 + v 2 ≤ - 2 u + 2

Cortando o - 2 u e passando o - 1 pro lado de lá...

u 2 + v 2 ≤ 1

Ou seja, como a gente pode notar na projeção, u   e   v variam dentro desse círculo de raio igual a 1!

Passo 5

Pois bem, não podemos prosseguir sem antes encontrar esse termo d S o que pela teoria é

d S = N → d u d v

Para encontrar o vetor normal, basta fazer

N → = - ∂ z ∂ u ,   - ∂ z ∂ v ,   1

Ou seja, z = - 2 u + 2

N → = 2 ,   0 ,   1

Logo

d S = N → d u d v

d S = 2 2 + + 0 2 + 1 2 d u d v

d S = 5 d u d v

Jogando tudo dentro da integral que temos que resolver

∬ S -   1 d S = ∬ D   5 d u d v

∬ S -   1 d S = 5 ∬ D   d u d v

Agora, quem é essa integral dupla aí? Sim! É a área de D ! Ué! Mas quem é D ??? Pow, D é a região de variação de u e v , logo D é aquele circulo de raio 1 que determinamos no passo 4!

Logo,

∬ S -   1 d S = 5   Á r e a   ( D )

∬ S -   1 d S = 5 π r 2

Como o raio r de D é 1

Á r e a S - = π 5

Passo 6

Letra c) Bem... Aqui não tem segredo, basta aplicar a fórmula de rotacional, se lembra?

r o t   F → = ∂ F 3 ∂ y - ∂ F 2 ∂ z ,   ∂ F 1 ∂ z - ∂ F 3 ∂ x ,   ∂ F 2 ∂ x - ∂ F 1 ∂ y

Sendo o campo vetorial F x ,   y ,   z = 2 x - y + 2 z ,   e 2 x + z - 2 ,   e z 2 + y , sendo cada uma dessa entrada F x , y   z = F 1 ,   F 2 ,   F 3 . Basta aplicar essas derivadas e correr para o abraço! Bora:

∂ F 3 ∂ y = ∂ e z 2 + y ∂ y = 1

∂ F 2 ∂ z = ∂ ( e 2 x + z - 2 ) ∂ z

Aplicando a regra da cadeia nessa daí...

∂ F 2 ∂ z = e 2 x + z - 2 ∙ ∂ 2 x + z - 2 ∂ z = e 2 x + z - 2

∂ F 1 ∂ z = ∂ 2 x - y + 2 z ∂ z = 2

∂ F 3 ∂ x = ∂ e z 2 + y ∂ x = 0

∂ F 2 ∂ x = ∂ e 2 x + z - 2 ∂ x

Aplicando novamente a regrada cadeia...

∂ F 2 ∂ x = e 2 x + z - 2 ∙ ∂ 2 x + z - 2 ∂ x = e 2 x + z - 2 ∙ 2

E por fim, podemos calcular a última derivada

∂ F 1 ∂ y = ∂ 2 x - y + 2 z ∂ y = - 1

Jogando todos esses resultados no vetor rotacional:

r o t   F → = 1 - e 2 x + z - 2 ,   2 - 0 ,   2 e 2 x + z - 2 - - 1

r o t   F → = 1 - e 2 x + z - 2 ,   2   ,   2 e 2 x + z - 2 + 1

Passo 7

Letra d) Cara, como a gente busca encontrar a integral de linha sobre a curva que entre as duas regiões. Bem, como a gente quer calcular a integral em uma borda de superfície, vamos usar a dica e utilizar Stokes!!!:)

  • Stokes nos pede uma curva fechada. Confere!
  • Devemos escolher uma superfície que tenha a curva como borda. Confere, a gente vai usar S - pela dica.
  • A superfície deve estar orientada positivamente. Confere!
  • Sem singularidades. Confere! A função F não tem problema em nenhum ponto.

Logo, podemos aplicar Stokes!

∫ γ   F d s = ∬ S -   r o t   F → �� n → d S

Se a gente busca encontrar o resultado dessa integral de linha, basta encontrar a da integral de superfície e fechou! Partiu?

Passo 8

Bem pela teoria sabemos:

∬ S -   r o t   F → ∙ n → d S = ∬ D   r o t   F → ∙ N → d u d v

Repare que nessa mudança, trocamos S - por D (a região circular onde varia os carinhas u e v ).

Substituindo esses dois caras, r o t   F → ∙ N → , que já encontramos teremos:

∬ D   1 - e 2 x + z - 2 ,   2   ,   2 e 2 x + z - 2 + 1 ∙ 2 ,   0 ,   1 d u d v =

Resolvendo o produto interno:

∬ D   2 - 2 e 2 x + z - 2 + 2 e 2 x + z - 2 + 1 d u d v =

Simplificando um pouquinho esses termos...

∬ D   3 d u d v = 3 ∬ D   1 d u d v

Essa integral, a gente já resolveu no item b e ela vale:

π

Logo, voltando par Stokes...

∫ γ   F d s = ∬ S -   r o t   F → ∙ n → d S

∫ γ   F d s = 3 π

Resposta

  2. Á r e a S - = π 5
  3. r o t   F → = 1 - e 2 x + z - 2 ,   2   ,   2 e 2 x + z - 2 + 1
  4. ∫ γ   F d s = 3 π

Exercícios de Livros Relacionados

Uma partícula se move ao longo dos segmentos de reta da origem aos pontos 1,0 , 0 ,1,2 , 1 ( 0,2 , 1 ) e de volta para a origem sob a influência do campo de forças F → = z 2 i → + 2 x y j → + 4 y 4 k
Use o teorema de Stokes para calcular ∬ S r o tF → ⋅ d S . F → x , y , z = x 2 z 2 i → + y 2 z 2 j → + x y z k → S é o hemisfério x 2 + y 2 + z 2 = 16 , y ≥ 0 , orientado em direção do eixo positivo d
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → = y i → + z j → + x k → S é o hemisfério x 2 + y ² + z ² = 1 ² ² , y ≥ 0 , orientado na direção posi
Use o teorema de Stokes para calcular ∬ S c u r lF → ⋅ d S . F → x , y , z = e x y c o s c o szi → + x 2 z j → + x y k → , S é o hemisfério x = 1 - y 2 - z 2 orientado na direção positiva do eixo x .
Use o teorema de Stokes para calcular ∫ C F → ⋅ d r → . Em cada caso, C é orientada no sentido anti-horário quando vista de cima. F → x , y , z = y z i → + 2 x z j → + ( e x y ) k → , C é a circunferê