Use o teorema de Stokes para calcular a integral de linha , em que
Em que é o limite da parte do plano no primeiro octante.
Passo 1
Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. Temos o plano limitado ao 1º octante, o que nos dá isso aqui:
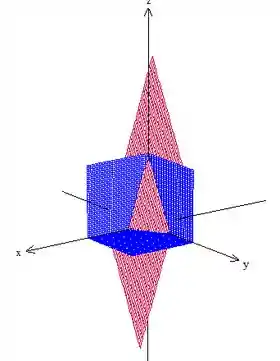
Como o plano é do tipo qualquer, para você ter uma ideia do gráfico, pode encontrar os pontos de interseção do plano com os eixos , e (fazendo , e ) e depois ligar esses pontos, formando esse triângulo que estamos vendo.
A questão pede para calcularmos a integral de linha em , que é a interseção do plano inclinado (em vermelho) com os planos azuis, que limitam o 1º octante. Como podemos ver, forma um triângulo. Percebeu?
Passo 2
O Teorema de Stokes nos diz isso aqui:
Ou seja, podemos substituir essa integral de linha sobre a curva por uma integral do rotacional de sobre uma superfície que tenha a curva como fronteira. No caso, vamos escolher esse retalho do plano mesmo, para simplificar as coisas!
Então, é o pedaço do plano que que está no 1º octante e é a própria curva , a fronteira do plano.Temos então:
Precisamos, então, calcular , sabendo que
Temos:
Passo 3
Agora vamos parametrizar a superfície .
Há infinitas superfícies com fronteira igual à curva do enunciado, mas para simplificar o problema, escolhemos o retalho do plano mesmo.
Qual será a melhor maneira para parametrizar o plano ? Vamos usar logo e como parâmetros, para ser mais simples:
Agora para descobrimos os intervalos de e , para descrever o domínio dessa função no plano . Para isso, precisamos imaginar a superfície vista de cima, no caso, temos o seguinte triângulo:
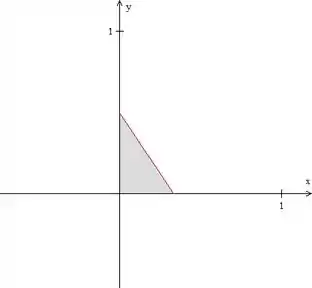
Essa reta vermelha é exatamente onde o plano corta o plano , portanto, sua equação é a seguinte:
Como vemos pela figura, varia desde o eixo até a reta vermelha e varia desde até o ponto onde a reta corta o eixo (onde ). Nesse ponto, temos:
Logo, a região pode ser escrita como:
Portanto, nosso plano é parametrizado por
Sendo que
Passo 4
Calcular
Como o problema não especifica a orientação da curva ou do vetor normal, vamos utilizar esse que encontramos mesmo.
Passo 5
Aplicar o Teorema
Passo 6
Agora vamos resolver essa integral aí. Integrando em relação a :
Agora em relação a :