Utilizando o Teorema de Stokes, transforme a integral numa integral de linha e a calcule, sabendo que , é parametrizada por , com , sendo a normal apontando para cima.
Passo 1
Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. A parametrização nos diz que:
Ou seja, um paraboloide, certo? Mas algo tem que limitar essa superfície, senão ela é infinita. Nós temos que
Ou seja,
Isso nos diz que o domínio dessa superfície é o círculo de raio centrado na origem. Portanto, temos isso aqui:
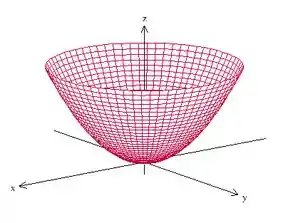
E o Teorema de Stokes nos diz o seguinte:
Ou seja, podemos substituir essa integral do rotacional de na superfície por uma integral de linha sobre a fronteira de . Como podemos ver pela imagem, essa fronteira é uma circunferência de raio .
Passo 2
Certo, agora precisamos calcular essa integral de linha. Como nós já estamos cansados de ver, o primeiro passo agora é achar uma parametrização para essa curva.
Bom, como se trata de uma circunferência de raio , temos que
Precisamos agora definir a coordenada dessa curva, ou seja, a altura da circunferência. Como ela faz parte do paraboloide, nada mais justo que substituir sua equação na dele, certo?
Pronto, descobrimos a altura dessa curva, agora precisamos parametrizá-la. Como se trata de uma circunferência, a melhor saída aqui é usar coordenadas polares
Como sabemos que o raio é igual a , podemos substituir . Como é dada uma volta completa temos . Lembrando que o é fixo em . Isso nos dá:
Passo 3
Agora precisamos calcular a derivada dessa parametrização:
Passo 4
Vamos, então, substituir na fórmula abaixo e escrever em função do parâmetro
Escrevendo a função vetorial
Em termos da parametrização
Temos
Substituindo na fórmula, temos