UFJF – Equações Diferenciais I – Avaliações Moodle – Atividade 2022.2 – 3
Considere a função e a série . Determine a afirmação verdadeira.
Escolha uma opção:
a. e a série converge.
b. e a série diverge.
c. e a série converge.
d. e a série converge.
e. e a série diverge.
f. e a série diverge.
g. e a série converge.
h. e a série converge.
i. e a série diverge.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função:
E uma série:
E pediu pra gente verificar a integral imprópria da função, , e verificar se a série converge ou diverge. Percebeu que a função é bem parecida com o termo geral da série? Como isso pode nos ajudar?
Bom, existe um teste chamado teste da integral, que nos diz que se é uma função contínua, positiva e descrecente em e se , então
- Se for convergente, então converge
- Se for divergente, então diverge
Beleza, então o que nós precisamos fazer é calcular a integral:
A gente apenas substituiu o no lugar do e jogou na integral, então vamos lá calcular agora!
Passo 2
Galera, a nossa integral é essa aqui:
Mas não seria legal se a gente pudesse transformar ela em uma integral com o resultado conhecido? Tipo essa aqui:
A notícia boa é que nós podemos fazer isso. Mas precisar chegar lá a gente vai precisar de alguns truques e substituições. Vamos começar fazendo:
Substituindo na integral original, temos:
Colando a constante pra fora da integral:
Passo 3
Falta pouco pra gente conseguir que nossa integral tenha essa cara , só falta a gente transformar aquele do denominador em . Pra isso, vamos usar o truque de chamar:
Substituindo na integral, temos:
Voltando pra variável , nós temos:
Jogando as constantes pra fora da integral:
E olha só, agora podemos resolver nossa integral:
Lembra que lá em cima nós definimos , então temos:
Vamos analisar os limites de integração agora. Quando a vai pra infinito, a nossa função se aproxima de e quando a nossa função é igual a . Isso fica mais claro no gráfico:
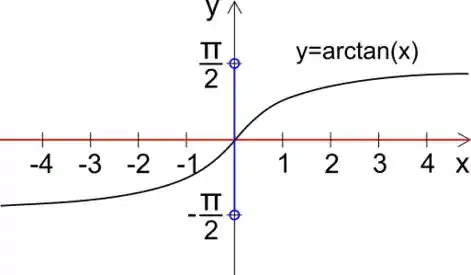
Substituindo, nós temos:
Simplificando:
Sendo assim, como nossa integral é convergente, a nossa série também converge pelo teste da integral. E nós podemos marcar a alternativa a.
E encerramos o exercício. Valeu, galera! 😉