Uma indústria de manufatura produz peças cujo diâmetro tem a seguinte especificação nominal . Pede-se:
- Qual a probabilidade de uma peça selecionada ao acaso, ter diâmetro entre e .
- Um comprador destas peças acertou a compra de um lote de peças. Qual a probabilidade da média dos diâmetros deste lote (denotada por ) ser ?
- Deste mesmo lote adquirido pelo fabricante, qual a probabilidade do maior dos diâmetros de todas as peças ser superior a ?
Passo 1
(a)
O exercício da uma v.a. com distribuição normal:
E pede primeiro que a gente calcule:
Primeiro padronizamos pra normal:
Vou dar uma ilustrada pra você ver se tá acompanhando direitin...
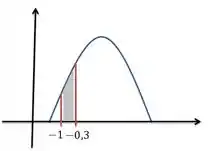
Passo 2
Aplicamos nossos conhecimentos da normal pra usar a tabela:
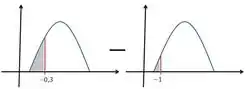
Trocando os sinais, já que não temos números negativos na tabela...
Graficamente fica mais fácil ainda de ver...
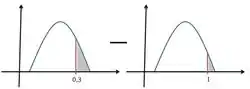
Invertendo pra gente usar a tabela que dá valores de ...
Procurando na tabela:
Passo 3
(b)
Agora temos um lote (amostra) com trinta peças:
E queremos uma probabilidade relacionada a média dos diâmetros dessa amostra .
Essa média tem uma distribuição normal também, só que um pouco diferente né...
Que vai ser então:
Agora podemos calcular o que a gente quiser.
Passo 4
Padronizando...
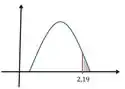
Usando a tabela...
Passo 5
(c)
Pra calcular o que é pedido a gente pode começar calculando a probabilidade de todos os diâmetros serem menores que .
A prob. de diâmetro ser menor que é dada por:
Pela tabela:
Passo 6
A probabilidade das peças terem diâmetro menor que será então:
Com isso, a prob. que a gente quer vai ser menos isso, concorda? A prob. do maior ser maior que é menos a prob. de ninguém ser maior que esse valor.