Suponhamos que o nível educacional de adultos de um certo país, apresenta distribuição normal com média de anos e variância de anos², determine:
- A probabilidade de que um adulto escolhido aleatoriamente, tenha entre e anos de tempo de estudo.
- Toma-se uma amostra de adultos, qual a probabilidade da média desta amostra ser menor que anos?
- Toma-se uma amostra de adultos, qual a probabilidade do menos idoso na amostra exceder anos de estudo?
Passo 1
(a)
Temos uma variável, que representa o nível educacional dos adultos do país, e a gente sabe que ela segue uma distribuição normal.
Certo?
A primeira coisa que o exercício pede é pra gente calcular:
Passo 2
Primeira coisa a fazer é padronizar isso, transformando pra ...
Vamos ver que região é essa, embaixo da gaussiana...
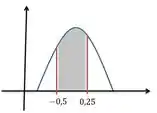
Então fica:
Vamos tirar o negativo dali, porque na tabela não tem negativo né...
E isso é o mesmo que:
Agora a gente pode olhar na tabela...
Passo 3
(b)
Fica esperto que agora não estamos mais falando da mesma variável, mas sim da média de uma amostra...
A distribuição normal pra média, tem o seguinte formato...
A média é a mesma, e a variância a gente divide por (número de elementos da amostra), que no caso é:
Vamos ter a seguinte distribuição então:
Passo 4
Agora a gente pode fazer o que o item pede, que é:
Mesmo modo de resolver, primeiro padronizamos:
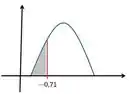
Tiramos o sinal de negativo...
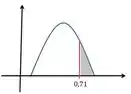
Concorda?
Que fica:
Aí é só procurar na tabela...
A resposta então é:
Passo 5
(c)
- Toma-se uma amostra de adultos, qual a probabilidade do menos idoso na amostra exceder anos de estudo?
Concorda comigo que dizer que o menos idoso vai exceder 15 anos de estudo, é a mesma coisa que falar que o mais novo vai estudar mais que 15 anos?
E nessa questão é esperado que a gente faça a seguinte análise: a idade das pessoas é proporcional ao tempo de estudo delas! Ou seja, pessoas mais velhas estudaram por mais tempo na vida que pessoas mais novas. Sacada chata né? Concordo!
Então, se queremos a probabilidade do mais novo ter estudado mais de 15 anos, em outras palavras, queremos a probabilidade de todos terem estudado mais que isso!
Primeiro podemos calcular a probabilidade de uma pessoa estudar mais de 15 anos:
Padronizando e usando nossas propriedades da Normal temos...
Mas nós temos pessoas e queremos que todas elas estudem mais de 15 anos, então vamos ter essa probabilidade elevada a :