Determine
Passo 1
Substituindo os valores de e :
Uma função me fornece o valor cuja tagente seja igual a . Repare que o termo dentro da arctangente tende pra .
Deste modo, temos que buscar qual valor cuja tangente vai para o infinito.
Passo 2
Lembra que a função tangente é uma razão de seno e cosseno?
Note, que quando o cosseno for zero, os valores de tangente vão tender ao infinito. E o cosseno é igual a zero, onde é qualquer número inteiro.
Vamos olhar o gráfico da função tangente para entender melhor seu comportamento:
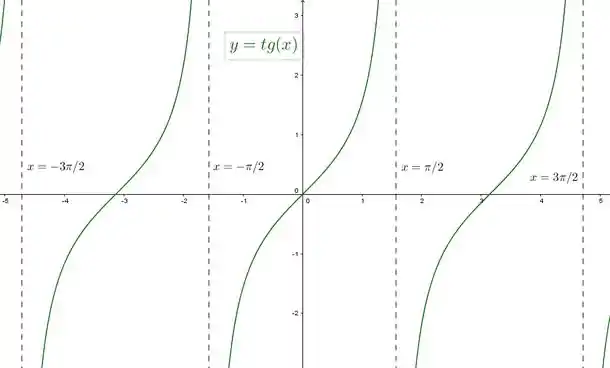
Repara que ela vai para infinito para .
Assim, temos
Botei as aspas porque não dá pra tratar o infinito como se fosse um número! Mas escrevendo a resposta bonitinha, temos que