Por meio de coordenadas polares, calcule a integral
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos pegar aqui a nossa integral:
Como queremos trabalhar com coordenadas polares, vamos dizer:
Show, com essas informações, a gente vai conseguir calcular.
Passo 2
Para começar, vamos montar um esboço da nossa integral:
Reparem que pela integral, temos que:
Vamos ter algo parecido com:
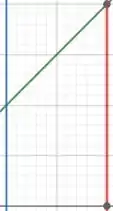
Com isso, a gente já consegue começar a mudar as coordenadas. Começando por :
Agora vamos para :
Por fim, vamos alterar a função dentro da integral:
Logo, teremos:
Passo 3
Agora vamos resolver a nossa integral:
Começando pela mais interna:
Ficando agora