Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 912345678101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Coordenadas polares

Calcule a seguinte integral:

∫ 1 2 ∫ 0 2 x - x 2 1 x 2 + y 2 3 / 2 d y d x

Passo 1

Bom, não dá pra integrar isso aí de cara, não é? Temos que mexer em alguma coisa nessa integral.

Os termos quadráticos no denominador da integral são um indicativo de coordenadas polares podem ser uma boa.

Vamos fazer, então:

x = r cos ⁡ θ

y = r   s e n θ

J = r

Passo 2

Vamos ver que região é essa aí, então.Temos 0 ≤ y ≤ 2 x - x 2 , ou seja, y varia desde 0 até a parte positiva da equação:

y 2 = 2 x - x 2

x 2 + y 2 - 2 x = 0

Completando esse quadrado, temos:

x - 1 2 + y 2 = 1

Essa é uma circunferência centrada em ( 1,0 ) . Podemos ver, também, que x varia desde 1 até 2 . Juntando essas informações, podemos esboçar a seguinte região:

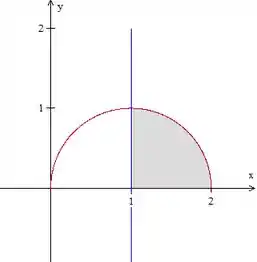
Pela figura, vemos que r varia desde a reta x = 1 até a circunferência, que, em coordenadas polares, será:

( r cos ⁡ θ ) 2 + ( r   s e n   θ ) 2 - 2 r cos ⁡ θ = 0

r 2 = 2 r cos ⁡ θ

r = 2 cos ⁡ θ

Para a reta, temos:

r cos ⁡ θ = 1

r = 1 cos ⁡ θ

Logo, 1 / cos ⁡ θ ≤ r ≤ 2 cos ⁡ θ . Podemos ver, pelo esboço do gráfico indicando a região de integração, que 0 ≤ θ ≤ π / 4 . Então, podemos escrever a região como:

D = r , θ 0 ≤ θ ≤ π 4 ; 1 cos ⁡ θ ≤ r ≤ 2 cos ⁡ θ

A integral passa a ser, então:

∫ 0 π / 4 ∫ 1 / cos ⁡ θ 2 cos ⁡ θ 1 r cos ⁡ θ 2 + r   s e n   θ 2 3 / 2 r d r d θ =

= ∫ 0 π / 4 ∫ 1 / cos ⁡ θ 2 cos ⁡ θ 1 r 2 d r d θ =

Passo 3

Agora vamos integrar em relação a r :

= - ∫ 0 π / 4 1 r 1 / cos ⁡ θ 2 cos ⁡ θ d θ =

= - ∫ 0 π 4 1 2 c o s θ - cos ⁡ θ d θ =

= ∫ 0 π / 4 cos ⁡ θ - 1 2 cos ⁡ θ d θ =

= ∫ 0 π / 4 cos ⁡ θ - 1 2 sec ⁡ θ d θ =

Passo 4

Agora em relação a θ :

= s e n   θ - 1 2 ln ⁡ | t g   θ + sec ⁡ θ | 0 π / 4 =

= 2 2 - 1 2 ( ln ⁡ 1 + 2 - l n ⁡ | 0 + 1 | ) =

= 2 2 - 1 2 ln ⁡ 1 + 2 - ln ⁡ 1 =

E como o ln ⁡ 1 = 0 , teremos finalmente:

= 2 2 - 1 2 ( l n ⁡ ( 1 + 2 )

Resposta

2 2 - 1 2 ln ⁡ ( 1 + 2 )

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}