Qual das alternativas exibe o valor correto da integral
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
Temos uma assombrosa integral pela frente. Temos duas opções: fazê-la diretamente ou podemos parar para analisá-la.
Mas afinal, como podemos analisar uma integral? Um bom começo é analisar os intervalos de integração. Mas por quê? Bom, pelos limites de integração podemos ter um esboço do nosso gráfico.
Vamos lá ver como é?! É mais ou menos nessa pegada:
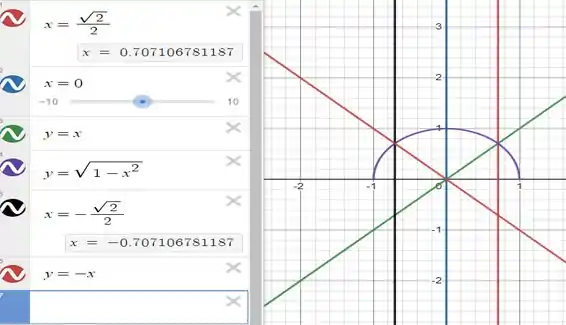
E veja como um problema em coordenadas cartesianas consegue assumir forma pola.
OK, Mogli... mas e o Kiko? (Kiko tenho a ver com isso?) huehuehe
Nós temos uma coordenada especifica para isso, chamada de coordenadas polares. Agora temos tudo que precisamos! Veja que se passarmos para coordenadas polares vamos deixar esse problema fácil fácil.
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
As coordenadas polares, como qualquer sistema de coordenadas, são formas de visualizar um gráfico. Como elas são?
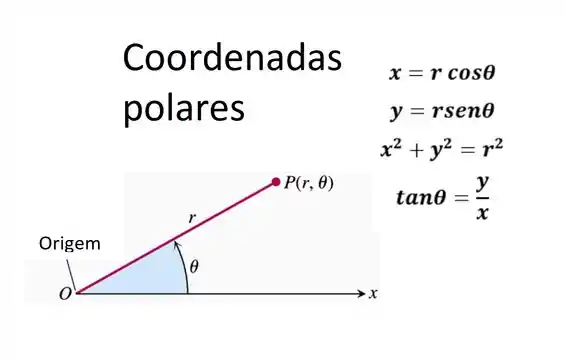
E agora observando suas variáveis podemos ver como que nossa integral fica.
E lembre-se, quando nós trocamos de variáveis é como se tivéssemos vendo o gráfico por outros olhos, ou melhor, por outro ângulo. Mas a vida seria um doce se pudéssemos apenas trocar nosso modo de ver. Na realidade nós precisamos considerar um termo de compensação, esse termo é o que nos permite transformar de uma coordenadas para outra! Geralmente ele é chamado de Jacobiano.
Ok, Mogli, mas como é o jacobiano das coordenadas polares?
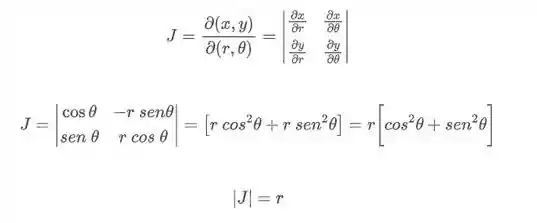
E como eu insiro o jacobiano da minha integral após as transformações de coordenadas?
Simples, veja:
Passo 3
Bom, vemos que temos na nossa função:
Mas como foi dito . Assim:
Mas e sobre os limites de integração? Lembra da nossa imagem do esboço? 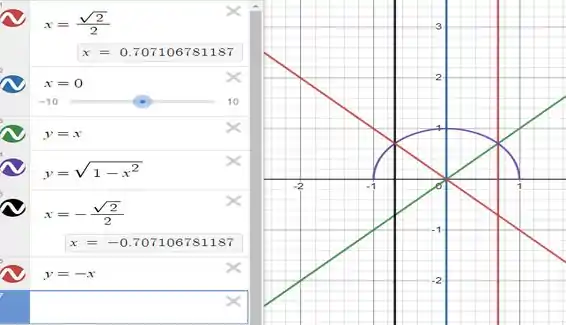
Vemos que o raio vai de 0 até 1, e que o ângulo vai de até . “Como eu sei disso, Mogli?”
Temos a função , certo? E temos que o raio é dado por , ok? Então:
Mas como r é o módulo distancia da origem até o ponot, só pode ser positiva, assim e como parte da origem
E para o ângulo, foi nos dado que , mas vemos que o que limita o o ângulo é a interseção da reta com as retas , assim temos que , logo , é simetrico de ambos os lados, logo .
Agora pronto... Temos a faca e o queijo na mão, bora finalizar?!
Passo 4
Temos então a nossa integral:
Integrando primeiro em nós temos que fazer uma substituição par deixar isso mais tranquilo, mas calma! Essa substituição é simples, veja:
Temos:
Mas podemos fazer
De forma que a derivada:
Veja que assim temos ao final:
E facilitamos e muito o nosso trabalho, certo?!
MAS, CALMA, JOVEM MANCEBO! Atente-se, quando nós fazemos alguma substituição, qualquer que seja, nós temos que ver como que os limites de integração estão nessa substituição, assim:
Assim a nossa integral fica:
Integrando em u:
Agora para veja que é constante para . Assim podemos fazer:
Integrando em , temos então:
Deixando igual a resposta nas alternativas:
Que alternativa é essa? A alternativa e)
E pronto, jovem mancebo, acabamos com o nosso trabalho. Obrigado por ter ficado até aqui, até a próxima!
Resposta
Alternativa e)