8 - Uma região é mostrada em cada um dos gráficos da figura abaixo. Decida se você deve usar coordenadas polares ou retangulares e escreva os limites de integração da integral iterada , onde f é uma função arbitrária qualquer contínua em R.

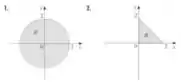
Na primeira figura, temos um círculo de raio

Acabamos de dizer que quando temos um círculo, temos que usar coordenadas polares.

Identificamos o método que vamos usar, mas e pra montar a integral, como fazemos?

Nossa integral é do tipo

Resta a gente identificar os valores para os limites de integração em e . Como descrito na integral, os valores dos limites em é dado pela variação do raio do círculo. Já é o ângulo que nossa região faz com a origem tendo como o ângulo , o semieixo positivo de .

Com essas afirmações, podemos tirar que

Com isso, nossa integral é

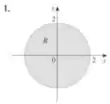
Agora vamos analisar a região

Temos que observar se tem alguma coisa que se parece com algo redondo.

Não né? Temos um triângulo, então temos que usar coordenadas retangulares.

Nesse caso os limites de integração são dados como o primeiro por curvas e o segundo por constantes. Por exemplo, se formos fazer , primeiro vamos observar as curvas que limitam os valores na horizontal.

Partindo do maior para o menor, vemos que partimos da reta e paramos em . Já com relação ao eixo , temos que partir de duas constantes, no caso do maior valor que é para o menor valor que é .

Se quisermos obter fazemos a mesma coisa só que escrevendo a reta como

Dessa forma, os limites de integração para essa região é

ou

Tranquilo? 👀

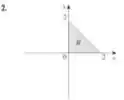
Analisando a região , temos

Vemos que a semelhança com a região anterior é muito grande, então vamos usar coordenadas retangulares também.

Porém os limites de integração são diferentes já que a região varia entre curvas diferentes.

Se formos calcular , vamos analisar a variação na horizontal. Podemos perceber que nossa região está variando entre a reta e

Já na vertical, a região varia entre e , aqui não precisamos considerar a curva pois já consideramos ela em .

Dessa forma, nossa integral será

ou

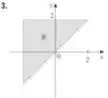
Para a região , temos

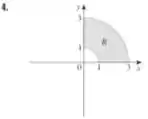
Neste caso, temos um semianel, ou seja, temos que aplicar coordenadas polares para calcular sua integral.

Como vimos antes, a integral polar tem a cara dessa forma

Com isso, podemos obter os limites de integração sem muitos problemas. Vemos que o raio está variando de forma constante para todo seu entre e . Já seu varia entre (semieixo positivo de até .

Com isso, nossa integral será

Interessante, não é? 😁

Analisando a região , temos

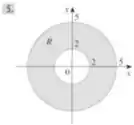
Na região anterior tínhamos um semianel, agora temos um anel completo, então vamos usar coordenadas polares novamente.

A integral de coordenadas polares é

Observando os dados que temos da região, vemos que seu raio varia entre e e seu ângulo entre e , já que ele faz uma volta completa na origem do sistema.

Com isso, nossa integral será

Por fim, analisando a região , temos

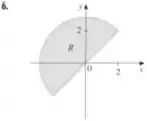
Para quem está com fome, temos um pastel, mas para quem não está, temos um semicírculo inclinado e centrado na origem.

Assim como os anteriores, vamos aplicar coordenadas polares.

Podemos ver que o raio varia entre e e o ângulo entre e já que o ângulo está sob o semieixo positivo de .

Ou seja, nossa integral é

Fim! Iae, o que achou? Responde Aí! 😁