Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFU, Sem Campus, Cálculo 2, Listas de C2 - Profª Ana Paula - Lista 7 - Integrais Duplas, Questão 15

Use coordenadas polares para resolver a integral ∫ 0 2 ∫ x 8 - x 2 1 5 + x 2 + y 2 d y d x .

Passo 1

Fala, galera! Vamos resolver essa questão!

O enunciado pediu pra gente calcular a integral iterada, usando as coordenadas polares. Olhando para os intervalos de integração, a gente vê que y varia da reta y = x até a a curva y = 8 - x 2 , que é a parte positiva da circunferência de centro na origem e raio 8 . E a gente vê que x varia de 0 até 2 . Então, nossa região de integração seria essa daqui:

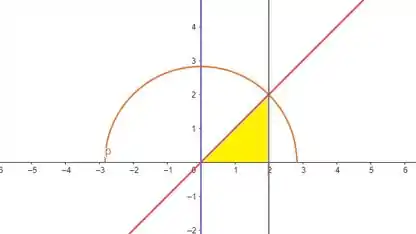
Mas como nós vamos usar as coordenadas polares, vamos precisar das equações de transformação:

x = r cos ⁡ θ

y = r sin ⁡ θ

Usando essas equações, vamos descobrir nosso novo integrando, com seus respectivos limites de integração, e calcular a integral em relação a r e θ .

Vamos lá!

Passo 2

Nós vimos no passo 1 que:

x ≤ y ≤ 8 - x 2

Pegando a parte da direita do intervalo e substituindo as equações de transformação para coordenadas polares, vamos ter:

y ≤ 8 - x 2

r sin ⁡ θ ≤ 8 - r 2 cos 2 ⁡ θ

Elevando ambos os lados ao quadrado:

r 2 sin 2 ⁡ θ ≤ 8 - r 2 cos 2 ⁡ θ

r 2 sin 2 ⁡ θ + r 2 cos 2 ⁡ θ ≤ 8

Usando a identidade trigonométrica cos 2 ⁡ θ + sin 2 ⁡ θ = 1 , temos:

r 2 cos 2 ⁡ θ + sin 2 ⁡ θ ≤ 8

r 2 ≤ 8

→ r ≤ 8

Olhando pra figura do passo 1 , a gente percebe que o nosso raio varia de 0 até 8 , também de acordo com o resultado que encontramos agora. Então, temos:

0 ≤ r ≤ 8

Além disso, no lado esquerdo do intervalo, nós temos a reta y = x , que vai ter um ângulo de inclinação θ = π 4 . Então, nosso ângulo vai variar assim:

0 ≤ θ ≤ π 4

Passo 3

Agora vamos dar uma olhadinha no nosso integrando, 1 5 + x 2 + y 2 . Passando pra coordenadas polares, vamos ter:

1 5 + x 2 + y 2 = 1 5 + r cos ⁡ θ 2 + r sin ⁡ θ 2

= 1 5 + r 2 ( cos 2 ⁡ θ + sin 2 ⁡ θ ) = 1 5 + r 2

Agora podemos montar nossa integral:

∫ 0 π / 4 ∫ 0 8 1 5 + r 2 r   d r d θ = ∫ 0 π / 4 ∫ 0 8 r 5 + r 2   d r d θ

Integrando primeiro em relação a r , temos:

∫ 0 π / 4 1 2 ln ⁡ ( 5 + r 2 )   0 8 d θ

Aplicando os intervalos de integração em r :

∫ 0 π / 4 1 2 ln ⁡ ( 5 + 8 2 ) - 1 2 ln ⁡ ( 5 + 0 2 )   d θ

= 1 2 ∫ 0 π 4 ln ⁡ 13 - ln ⁡ 5 d θ

Usando as propriedades de logaritmo e colocando a constante do lado de fora da integral:

= 1 2 ln ⁡ 13 5 ∫ 0 π / 4 d θ

Agora integrando em relação a θ :

1 2 ln ⁡ 13 5 θ 0 π / 4

E aplicando os limites de integração em θ :

1 2 ln ⁡ 13 5 π 4 - 0

= π 8 ln ⁡ 13 5

Valeu, galera! Até a próxima! 😉

Resposta

π 8 ln ⁡ 13 5

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}