Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 111234567891012131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Coordenadas polares

Utilize coordenadas polares para combinar a soma

∫ 0 1 / 2 ∫ 0 x x   d y d x + ∫ 1 / 2 1 ∫ 0 1 - x 2 x   d y d x

Em uma única integral. Em seguida, calcule essa integral.

Passo 1

Bom, antes de tudo, vamos desenhar essas regiões de integração, para entender melhor o que está acontecendo. Temos:

D 1 = { ( x , y ) | 0 ≤ y ≤ x ,   0 ≤ x ≤ 1 / 2 }

D 2 = { ( x , y ) | 0 ≤ y ≤ 1 - x 2 ,   1 / 2 ≤ x ≤ 1 }

Para a primeira região, temos y entre as retas y = 0 e y = x e x variando entre 0 e 1 / 2 . Graficamente:

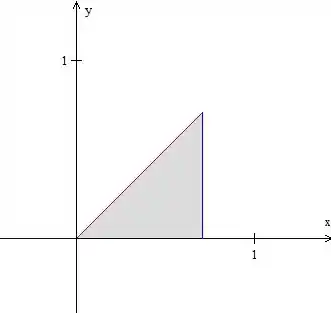
Para a segunda região, temos y entre y = 0 e y = 1 - x 2 . Ok, a primeira equação e uma reta, mas e a segunda? Se a gente elevar os dois lados ao quadrado, temos:

y 2 = 1 - x 2

x 2 + y 2 = 1

Isso é uma circunferência de raio 1 , certo?? Como originalmente tínhamos y = r a i z , sabemos que y ≥ 0 , ou seja, trata-se de um arco de circunferência. Sacou?

Sabemos também que 1 / 2 ≤ x ≤ 1 para essa região. Agora vamos desenhar isso tudo:

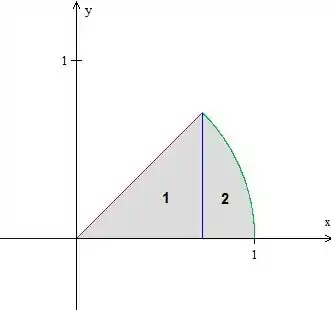
Desenhamos as duas regiões juntas porque nossso objetivo é formar uma única integral. Bom, já deu pra perceber que isso aí é um setor, não é? Temos 0 ≤ r ≤ 1 e θ desde zero até a reta vermelha.

Passo 2

Agora, vamos descrever essa região em coordenadas polares. Como já vimos:

0 ≤ r ≤ 1

E o ângulo θ varia desde θ = 0 até a reta y = x . Bom, para descobrir que ângulo ela representa, basta fazer a mudança polar na sua equação:

x = r cos ⁡ θ

y = r   s e n   θ

Temos:

r   s e n   θ = r cos ⁡ θ

t g   θ = 1

θ = π / 4

Logo, temos 0 ≤ θ ≤ π / 4 .

Passo 3

Agora vamos montar a integral em coordenadas polares, fazendo a substituição:

x = r cos ⁡ θ

y = r   s e n   θ

J = r

∫ 0 1 / 2 ∫ 0 x x   d y d x + ∫ 1 / 2 1 ∫ 0 1 - x 2 x   d y d x = ∫ 0 π / 4 ∫ 0 1 r cos ⁡ θ r d r d θ

Show? Temos, então:

= ∫ 0 π / 4 ∫ 0 1 r 2 cos ⁡ θ d r d θ =

Passo 4

Agora é só resolver isso aí:

= 1 3 ∫ 0 π / 4 r 3 cos ⁡ θ 0 1 d θ =

= 1 3 ∫ 0 π / 4 cos ⁡ θ d θ =

= 1 3 s e n   θ 0 π / 4 =

= 2 6 =

Resposta

2 6

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}