Utilize coordenadas polares para calcular
Onde
Passo 1
Bom, antes de tudo, vamos desenhar essa região , para ter uma ideia melhor do que está acontecendo. Queremos a parte com do círculo de raio :
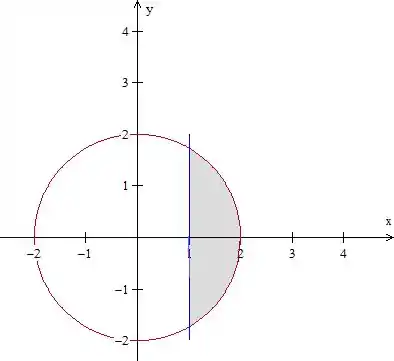
Temos, então, essa região cinza.
Passo 2
Agora, vamos descrever essa região em coordenadas polares.
Como o raio vai desde a reta até a circunferência de raio , vamos fazer a mudança polar na reta:
Logo
Agora, para achar o intervalo de , precisamos descobrir onde a reta corta a circunferência, ou seja, onde:
Isso ocorre se
Logo, temos .
Passo 3
Agora vamos montar a integral em coordenadas polares, fazendo a substituição:
Temos, então:
Passo 4
Agora é só resolver isso aí:
Resposta
Exercícios de Livros Relacionados
Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}