Unicamp, Cálculo 2, 2019.2, P2, Questão 2.
Calcule a integral
Onde é a região no primeiro quadrante limitada pelas retas , , e pelos círculos e .
Passo 1
Então pessoal, vamos começar fazendo um esboço da região que estamos integrando.
Primeiro, a gente vai ter dois círculos, um de raio :
E um de raio :
Então:
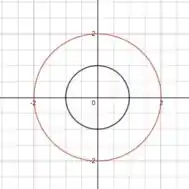
Mas o enunciado pediu pra olhar só para o primeiro quadrante. E só na região entre as retas e , então:
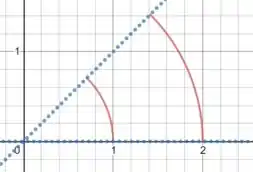
Beleza, é essa região aí que queremos analisar.
Vale lembrar, aproveitando o desenho, que essa reta faz um ângulo de com o eixo horizontal.
Passo 2
Beleza, já que estamos lidando com círculos, vamos passar o problema para coordenadas polares. Pra isso vamos usar essas transformações aqui:
Então a nossa função, que é simplesmente , vai ficar assim:
E o Jacobiano vai seguir a fórmula de sempre:
A parte difícil vem na hora de definir os limites de integração. A gente pode fazer isso só olhando o desenho:
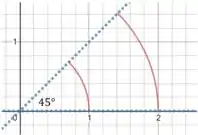
Pra preencher essa área aí, o nosso raio tem que ir desde o círculo de raio () até o círuclo de raio ), então:
E o ângulo tem que ir desde o até o :
Passo 3
Então já temos tudo pra montar a integral:
Ou seja:
E dá pra separar isso em um produto de duas integrais:
E então vamos calcular cada uma delas. Primeiro, lembrando que a integral de é :
E a segunda é simplesmente a integral de um polinômio:
Então, juntando as duas:
Pronto! Esse é o valor da integral.
Resposta
A integral vale .