Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 261234567891011121314151617181920212223242527282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 4: Calcule a integral dada, colocando-a em coordenadas polares:

∬ R   cos ⁡ x 2 + y 2 d A

Onde R é a região acima do eixo x e dentro da circunferência x 2 + y 2 = 9 .

Passo 1

Se o problema nos pediu para passar a integral para coordenadas polares é isso que devemos fazer. Lembre-se que essa mudança faz:

x = r cos ⁡ θ

y = r sin ⁡ θ

O Jacobiano dessa mudança é:

J = r

Outra equação que é muito linda é que se você somar os quadrados dessas coordenadas polares:

x 2 + y 2 = r 2       ( e q u a ç ã o   d a   c i r c u n f e r ê n c i a )

Assim...

∬ R   cos ⁡ x 2 + y 2 d A = ∬ R r θ   cos ⁡ r 2 ⋅ J d r d θ =

∬ R r θ   cos ⁡ r 2 r   d r d θ

Aqui eu só tenho duas observações mesmo que preciso que você fique atento quando fazemos essa mudança: primeiro que devemos multiplicar a função de integração pelo Jacobiano.

Segundo que como as variáveis de integração mudou, costumamos mudar também o nome da região de R para R r θ . Mas isso, repito, é apenas uma mudança de nome para indicar que agora a região deve ser representada em coordenadas polares.

Passo 2

Bem, mas o nosso próximo passo aqui é justamente descrever essa região de integração. Do enunciado tiramos que a nossa região R é o semicírculo de raio 3 ...

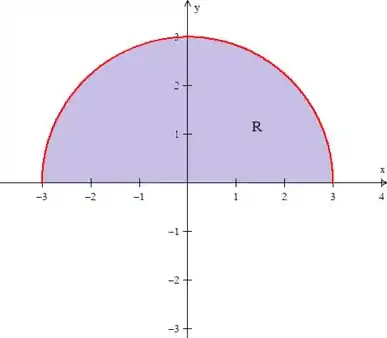
Lembrando que θ varia sempre do eixo x girando no sentido anti-horário e o raio, enquanto o raio varia da origem até a curva...

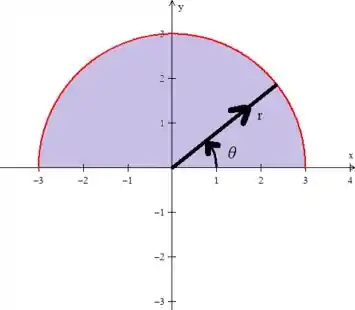
Podemos falar aqui que temos que ter um θ varaiando de 0 a 180 ° :

0 ≤ θ ≤ π

Enquanto o nosso r varia de 0 até o raio máximo que é o próprio raio da circunferência:

0 ≤ r ≤ 3

Assim:

∬ R r θ   cos ⁡ r 2 r   d r d θ = ∫ 0 π ∫ 0 3 cos ⁡ r 2 r   d r d θ

Bora calcula-la?

Passo 3

Vamos começar a calcular a integral em relação a r fazendo uma mudança...

r 2 = u                 →

d u = 2 r   d r       o u           r d r = d u 2

Não se esquecendo dos limites...

r = 0             →                 u = 0 2 = 0

r = 3             →                 u = 3 2 = 9

∫ 0 π ∫ 0 3 cos ⁡ r 2 r   d r d θ = ∫ 0 π ∫ 0 9 cos ⁡ u d u 2 d θ =

1 2 ∫ 0 π   sin ⁡ u   0 9 d θ = 1 2 ∫ 0 π sin ⁡ 9 - sin ⁡ 0 d θ =

sin ⁡ 9 2 ∫ 0 π d θ =

Integrando esse cara aí...

sin ⁡ 9 2 ⋅ π

Resposta

sin ⁡ 9 2 ⋅ π

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}