Calcule a integral abaixo
Passo 1
Bem, a princípio, esse problema pode não parecer simples de identificar o método de integração, porque já vou te avisando que ele não está assim tão na cara mesmo não. Mas nada que, com a prática, você não comece a identificar.
Bom, repara comigo que uma substituição simples não vai resolver o seu problema, porque dentro da raiz, você tem uma diferença com um termo . Quando derivar essa soma, vai ficar com um termo em . E não tem nada de fora da raiz (fail!).
Mas olha só: eu tenho um termo dentro da raiz e um termo . Isso me faz lembrar, bem lá no fundo, substituição trigonométrica. Ok, eu sei que você pensou: “Essa menina tá viajando aí, porque eu não tenho nada que pareça ou ”.
Calma, como diz o ditado: nem tudo é o que parece ser.
Lembra daquela fórmula marota para calcular coisas do tipo ?
Lembra que é assim?
Olha bem para essa função:
Repara que falta um numerozinho ali para ela ficar com essa carinha de e poder ser substituída por
Então, nesse caso, você pode completar o quadrado! E como você faz isso?
Pensa o seguinte (sem se preocupar com o sinal, por enquanto): você quer chegar em algo bonitinho do tipo .
Você já tem o e a parte do .
Se você fizer , você descobre que ser
Se você quer chegar em algo do tipo , quem está faltando é o , concorda? Se o , o seria .
Você tem que fazer aquele aparecer ali, mas, obviamente, você não pode alterar a função. Se aquele não está no enunciado, você não pode simplesmente coloca-lo ali porque sem ele não dá para resolver. E aí?
Passo 2
Antes de responder isso, vamos pensar no sinal e colocar na forma já bonitinha:
Temos , que podemos reescrever como , beleza?
Vamos colocar o dentro disso aí? Assim:
Só que, como eu falei, aquele 16 não estava ali. Então o que a gente faz para não alterar a função original. Se eu desmembrar aquele termo ali em cima:
No final, esse 16 que eu coloquei aí para completar o quadrado ficou , certo?
Se eu somar um termo e diminuir o mesmo termo, eu não estou alterando nada, certo? Porque no final, o termo menos ele mesmo será zero, não é mesmo?
Então... Olha que lindo!
Eu posso simplesmente somar um :
No final eu chegarei à expressão original:
Você pode não estar entendendo ainda e achando que estou rodando em círculos e colocando algo que vou tirar depois. Mas o meu objetivo não é tirar o . É deixa-lo ali. Só que sem alterar a função original. O vai me fazer ser capaz de resolver a questão. Observa:
Agora eu tenho:
Percebeu que mágico? Você adicionou algo que vai te ajudar pra caramba sem alterar a função original (pode abrir aquele quadrado e conferir quantas vezes quiser que o que você tem ali vai ser sempre !).
Passo 3
Ufa! Fiz tudo isso, mas ainda temos que resolver essa integral.
Vou chamar aquele termo de , só para facilitar a visualização do problema aqui, ok?
Se eu fizer:
Olha só como fica a integral:
E aí? Substituição trigonométrica gritando para ser usada?
Sim, temos aquele caso de típico de substituição trigonométrica com uma expressão do tipo .
Só que nesse caso, o que eu tenho que chamar de não é e sim o , saca?
Então a substituição que vou fazer é a seguinte:
Passo 4
Agora vamos partir para a resolução propriamente dita. Já identificamos qual caso usar. O próximo passo é identificar quem é o e, a partir disso, calcular e substituir na integral.
Temos
Portanto, temos:
Substituindo na integral dada:
Passo 5
Agora devemos resolver a integral na variável . Para isso, vamos utilizar a propriedade trigonométrica:
Passo 6
Agora que resolvemos a integral em , vamos voltar para . Montamos aquele triângulo maroto para des-substituir o para , lembrando que nesse caso, o triângulo fica com essa cara aqui, ó:
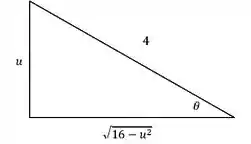
A partir desse triângulo, tiramos todas as relações de que precisamos. Nesse caso, precisamos do valor de e de . Vale lembrar que:
Portanto, precisamos calcular as relações e
Substituindo isso no resultado em que havíamos encontrado e lembrando que é uma integral indefinida, portanto, não devemos esquecer a constante , beleza? Se liga aí para não dar bobeira!
Chamei a constante aí em cima de porque essa ainda não é a resposta definitiva. Voltamos para , mas a integral que tínhamos inicialmente era em . Esse aí veio daquela substituição esperta que fizemos para faciliar nossa vida.
Agora temos que voltar para . Lembrando que fizemos :