Resolva a integral definida:
Passo 1
Você pode se assustar ao olhar essa integral, até porque ela tem um módulo ali, o que, por si só, já causa um certo desconforto.
Mas olha só: quando você tem módulo, o importante é você lembrar da definição de módulo.
Dependendo do intervalo, terá comportamentos diferentes. Mas repara só: o intervalo de integração que ele deu vai de a , ou seja, são sempre valores negativos. O que significa que nesse intervalo de integração que ele deu, será sempre igual a , concorda? Então vou escrever assim:
Só mais uma coisinha: repara que o limite inferior é, que é maior que o limite superior . Como tenho um menos ali na frente do , posso aproveitar isso para usar aquela propriedade de integrais definidas que me permite mudar os limites de integração. Isso vai evitar que eu fique carregando aquele menos ali na frente do .
Passo 2
Beleza. Agora eu tenho uma integral meio esquisita para resolver. Vamos esquecer os limites de integração por enquanto e pensar em como achar a primitiva dessa função, ok?
Repara bem nessa integral. Você vê que temos uma raiz quadrada e que tem um ali menos uma constante. Isso não te lembra nada? Nadinha mesmo? Vou te dar uma dica: .
Ok. Problema: Tem uma constante ali na frente do e como essa constante é diferente da constante que está sendo subtraída, eu não posso coloca-la em evidência. Mas na matemática nada se cria, nada se perde e, com sorte, tudo se transforma em algo útil e mais bonito.
Que tal manipular aquela expressão ali dentro da raiz para que ela fique com essa carinha de ?
Vamos fazer
Aí a integral fica assim:
E agora? Vamos fazer a substituição trigonométrica!
Eu sei que você deve estar pensando: poxa, entender eu até entendi (ou aceitei, porque, né) mas eu nunca ia pensar nisso sozinho(a). Calma, essas coisas são questão de prática. E esses exercícios de fixação têm como objetivo de dar alguns bizus de coisas com as quais você pode se deparar na sua longa trajetória pelo mundo do Cálculo.
Fazendo mais exercícios, você vai ganhando bagagem para reconhecer essas pegadinhas, mesmo que nos primeiros você tenha que dar aquela coladinha, entendeu?
Bom, lembra que quando temos uma integral definida nós podemos tanto resolver a indefinida e depois utilizar o Teorema Fundamental do Cálculo quanto substituir direto os limites de integração em função da nova variável?
Então, na substituição simples, meio que tanto faz, mas no caso de substituição trigonométrica, vou te falar que não recomendo muito você tentar substituir os limites em função da variável . É melhor você esquecer os limites, calcular a indefinida em função de , voltar ara e aí substituir os limites, beleza?#Ficadica #Confia
Passo 3
Passado o susto inicial, vemos que temos uma integral que será resolvida pelo método da substituição trigonométrica, aquele caso em que temos .
O próximo passo é identificar quem é o e, a partir disso, calcular e substituir na integral.
Temos
Para escrever na forma , podemos escrever:
Portanto, temos:
Agora derivando
Substituindo na integral:
Lembrando que
Voltando para a integral
Passo 4
Agora devemos resolver a integral na variável . Essa integral é molezinha, amigo, tirar doce de criança:
Passo 5
Agora que já resolvemos a integral em , temos que voltar para . Então montamos aquele triângulo espertinho para des-substituir o para :
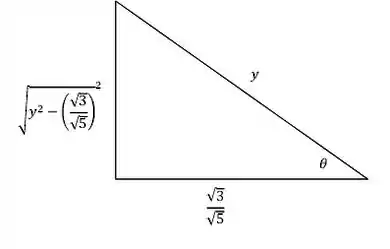
Passo 6
A questão ainda não acabou (todos choram). Queremos a integral definida. Achamos a primitiva. Agora temos que aplicar os limites de integração:
Isso é equivalente a escrever assim: