Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 451234567891011121314151617181920212223242526272829303132333435363738394041424344464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Substituição Trigonométrica

Calcule as seguintes integrais indefinidas:

a ∫ x 5 3 + x 2 d x

Passo 1

Tá, essa raiz quadrada com x 2 somado a constante é um indicador direto do método da Substituição Trigonométrica. Essa caso, pela nossa tabelinha da teoria, seria o da Tangente.

x = a tg ⁡ ( θ ) → d x = a sec 2 ⁡ ( θ ) d θ ; a = 3

∫ x 5 3 + x 2 d x = ∫ 3 tg ⁡ θ 5 3 + 3 tg ⁡ θ 2 3 sec 2 ⁡ θ d θ

= 3 5 3 ∫ tg ⁡ θ 5 3 + 3 tg 2 ⁡ θ sec 2 ⁡ θ d θ

= 3 3 ∫ tg ⁡ θ 5 3 sec 2 ⁡ θ sec 2 ⁡ θ d θ

= 27 ∫ tg ⁡ θ 5 3 sec ⁡ ( θ ) sec 2 ⁡ θ d θ

= 9 3 ∫ tg ⁡ θ 5 sec ⁡ θ d θ

Passo 2

Bom, e para resolver essa integral trigonométrica aqui? Na teoria dessas integrais a gente coloca esse caso aqui como sendo o caso 5 , onde a integral tem tangente com expoente ímpar. Nessa situação, vamos guardar um tg ⁡ θ . sec ⁡ θ , que é derivada da secante, e abrir o resto das tangentes em secantes:

9 3 ∫ tg ⁡ θ 4 tg ⁡ θ sec ⁡ θ d θ

= 9 3 ∫ sec 2 ⁡ θ - 1 2 tg ⁡ θ sec ⁡ θ d θ

= 9 3 ∫ 1 - 2 sec 2 ⁡ θ + sec 4 ⁡ θ tg ⁡ θ sec ⁡ θ d θ

u = sec ⁡ ( θ ) → d u = tg ⁡ θ sec ⁡ θ d θ

= 9 3 ∫ 1 - 2 u 2 + u 4 d u = 9 3 u - 2 u 3 3 + u 5 5

= 9 3 sec ⁡ ( θ ) - 2 sec ⁡ θ 3 3 + sec ⁡ θ 5 5

Passo 3

Bom, agora trazemos aquele triângulo maroto para des-substituir o θ para x , lembrando que lá em cima tínhamos tg ⁡ ( θ ) = x 3 :

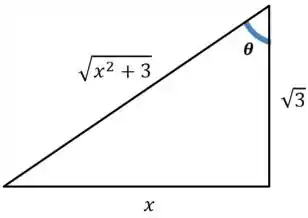
A partir dele, sec ⁡ ( θ ) = x 2 + 3 3 . Substituindo isso no reultado:

9 3 x 2 + 3 3 - 2 x 2 + 3 3 3 3 + x 2 + 3 3 5 5

= 9 x 2 + 3 - 2 x 2 + 3 3 + x 2 + 3 5 5 + C

Resposta

∫ x 5 3 + x 2 d x = 9 x 2 + 3 - 2 x 2 + 3 3 + x 2 + 3 5 5 + C

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x