Calcule a seguinte integral:
Passo 1
O termo vai ser a nossa deixa pra usar uma substituição trigonométrica. Mais especificamente, a substituição
Assim:
Daí a integral vai ficar:
Passo 2
Vamos escrever essa integral assim:
O que vai dar:
Passo 3
Mas ainda temos que voltar pra variável . Temos que
Montando o nosso triângulo retângulo:
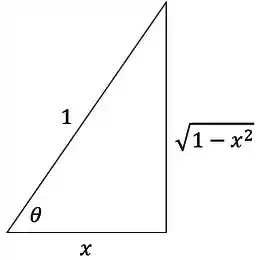
Daí podemos ver que
E a secante é:
Passo 4
Show, então juntando tudo, a integral vai dar: