Use substituição trigonométrica para calcular a integral dada.
Passo 1
Bem, ele disse que é para usar substituição trigonométrica, então vamos usá-la. Porém, o integrando ainda não está na forma perfeita para usarmos esse método (Nota-se, né? A equação está zuada...).
Logo, o primeiro passo será manipular o integrando para encontrarmos um dos casos de integração por substituição trigonométrica:
Talvez, para chegarmos lá, iremos ter que usar uma substituição antes. Vamu vê.
Passo 2
Vamos começar completando quadrados
Mas como?
Compara com o produto notável
Precisamos somar e subtrair
Passo 3
Vamos precisar usar primeiro a substituição
Precisamos calcular sua diferencial
Substituindo
Passo 4
Agora sim! Vamos seguir os passos do método de integração por substituição trigonométrica:
1. Identificar o caso da substituição trigonométrica e o valor de .
O caso é . E além disso
2. Aplicar a substituição recomendada e calcular .
Temos que fazer , para .
3. Substituir na integral dada.
Passo 5
4. Resolver a integral na variável .
Separado essa integral em duas vamos ter
Lembrando que
A integral fica
Passo 6
Vamos resolver primeiro a integral
Podemos fazer a substituição
Calculando a diferencial
Vamos agora deixar igual ao termo que está na integral
E já está exatamente assim na integral, vamos agora substituir na integral
Resolvendo a integral
Desubstituindo vamos ter
Passo 7
Vamos resolver a outra integral agora
Podemos fazer a substituição
Calculando a diferencial
Dando aquela arrumada para encontrar algo parecido com algo da integral
vamos agora substituir na integral
Resolvendo a integral
Desubstituindo vamos ter
Passo 8
Vamos ter então o seguinte resultado para a integral
Podemos juntar essas constantes em uma só e ter
Vamos abrir aquele para termos algo que depende de seno e cosseno. Basta lembrar que
Vamos ter
5. Usar o triângulo retângulo para converter o na variável inicial.
Fizemos que .
Sabemos que
Assim, , e
Repare que o lado do triângulo que falta sempre será igual à expressão do caso de substituição do início do problema.
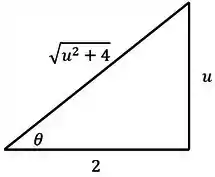
Logo,
Lembrando também que para acharmos usamos
Substituindo:
Passo 9
Temos a resposta em , precisamos desubstituir o valor de pelo de , lembrando que