Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Taxa Relacionada

Ver Teoria
Exercício 170123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFCG, Sem Campus, Cálculo Diferencial e Integral I, Listas Cálculo 1 - UAMat - Lista 4 - Aplicação de Derivadas, Questão 3b.

Determine os extremos relativos, os intervalos de crescimento e decrescimento das seguintes funções:

  1. f x = x 3 - 3 x 2 - 9 x + 19
  2. f x = 3 x 4 - 4 x 3 - 24 x 2 + 48 x

Passo 1

Vamos analisar a função f x = 3 x 4 - 4 x 3 - 24 x 2 + 48 x  

Extremos relativos são os pontos de máximo e mínimo!

Encontraremos os pontos críticos da função, onde a derivada primeira é igual a zero ou não existe. A derivada primeira da função é f ' x = 12 x 3 - 12 x 2 - 48 x + 48

Vamos encontrar os pontos críticos resolvendo f ' x = 0

12 x 3 -   12 x 2 -   48 x   +   48   =   0

Podemos simplificar a equação dividindo todos os termos por 12:

[ x 3 -   x 2 -   4 x   +   4   =   0 ]

Agora, vamos fatorar a equação:

[ x 2 ( x - 1 ) -   4 x   -   1 =   0 ]

Isso nos dá:

[ x   -   1 x 2 -   4 =   0 ]

Resolvendo para x

x   -   1   =   0 ⇒   x   =   1

x 2 -   4   =   0   ⇒ x 2 =   4   ⇒ x   =   ± 2

Portanto, temos três pontos críticos:   ( x   =   - 2 ) ,   ( x   =   1 ) ,   e   ( x   =   2 ) .

Passo 2

Agora, vamos determinar os intervalos de crescimento e decrescimento. Para fazer isso, podemos usar a derivada primeira f ' x e os pontos críticos que encontramos.

Vamos criar uma tabela de sinais para f ' ( x ) nos intervalos determinados pelos pontos críticos:

Agora, vamos escolher um valor de teste em cada intervalo e determinar o sinal de f ' ( x ) nesse intervalo. Vamos usar x = - 3 para o intervalo ( - ∞ ,   - 2 ) ,   ( x   =   0 ) para o intervalo ( - 2 ,   1 ) , ( x   =   1.5 ) para o intervalo 1 ,   2 ,   e ( x   =   3 ) para o intervalo ( 2 ,   + ∞ ) .

Para x = - 3

f ' - 3 =   12 - 3 3 -   12 - 3 2 -   48 - 3 +   48   =   - 432   <   0

Para x = 0

f ' 0 =   12 0 3 -   12 0 2 -   48 0 +   48   =   48   >   0

Para x = 1.5

f ' 1.5 =   12 1.5 3 -   12 1.5 2 -   48 1.5 +   48   =   - 18   <   0

Para   x = 3

f ' 3 =   12 3 3 -   12 3 2 -   48 3 +   48   =   432   >   0

Agora, podemos preencher a tabela de sinais:

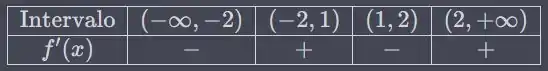
Passo 3

Agora, usando a tabela de sinais de f ' x , podemos determinar os intervalos de crescimento e decrescimento da função f ( x )

- A função f ( x ) é crescente nos intervalos onde f ' x > 0 , ou seja, nos intervalos ( - 2 ,   1 )   e   ( 2 ,   + ∞ ) .

- A função f ( x ) é decrescente nos intervalos onde f 1 x > 0 , ou seja, nos intervalos ( - ∞ ,   - 2 )   e   ( 1 ,   2 ) .

Agora, vamos determinar os extremos relativos. Para isso, precisamos analisar o comportamento de f ( x ) nos pontos críticos.

- No ponto crítico x = - 2 , a função muda de decrescente para crescente. Portanto, há um ponto de mínimo local nesse ponto.

- No ponto crítico x = 1 , a função muda de crescente para decrescente. Portanto, há um ponto de máximo local nesse ponto.

- No ponto crítico x = 2 , a função muda de decrescente para crescente. Portanto, há um ponto de mínimo local nesse ponto.

Resumo:

- A função f ( x ) cresce nos intervalos ( - 2 ,   1 )   e   ( 2 ,   + ∞ ) .

- A função f ( x ) decresce nos intervalos ( - ∞ ,   - 2 )   e   ( 1 ,   2 ) .

- A função tem pontos críticos em ( x = - 2 ) ,   ( x = 1 ) ,   e   ( x = 2 ) .

- Há um ponto de máximo local em x = 1

- Há pontos de mínimo local em x = - 2   e   x = 2 .

Resposta

Vide a explicação.

Exercícios de Livros Relacionados

20. Caminhão na estrada O gráfico a seguir mostra a posição de um caminhão que percorre uma estrada. O caminhão parte em t = 0 e retorna 15 h mais tarde, em t = 15.a. Use a técnica descrita no Exemplo
(a) Encontre a taxa de variação média da área de um círculo em relação ao seu raio r quando r varia de i 2a3i i2a2,5i i i 2a2,1 (b) Encontre a taxa de variação instantânea quando r = 2 (c) Mostre que
O número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função n = f t = a 1 + b e - 0,7 t Em que t é med
O rendimento total recebido da venda de x carteiras é R x = 200 x - 1 3 x 2 c) Ache o rendimento real da venda da trigésima primeira carteira.
A quantidade de carga Q , em coulombs (C), que passa através de um ponto em um fio até o instante t (medido em segundos) é dada por Q t = t 3 - 2 t 2 + 6 t + 2 Encontre a corrente quando (a) t = 0,5 s