UERJ, Sem Campus, Cálculo I, Listas de C1 - Profº Rubens Sucupira - Lista 3, Questão 54
Um peso está preso a uma das extremidades de uma corda de de comprimento que passa por uma polia situada a acima do solo. A outra extremidade da corda, que se encontra esticada, está presa a um caminhão por um ponto situado acima do solo. Sabendo que o caminhão se afasta horizontalmente a uma velocidade de , determine a taxa de variação da altura do peso no instante em que o mesmo estiver a acima do solo.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um sistema com uma corda de de comprimento, que suporta um peso em uma extremidade e está ligada a um caminhão na outra extremidade. A corda passa por uma polia que está a uma altura de do solo e nós sabemos que o caminhão se movimenta com uma velocidade . Então, a medida que o caminhã se afasta, ele puxa o peso da ooutra extremidade da corda pra cima.
Nós precisamos determinar a taxa com que esse peso sobe, ou seja, a variação de sua altura em relação ao tempo, . Vamos dar uma olhadinha no nosso sistema:
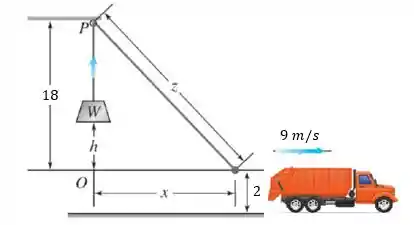
Observe que a altura da roldana acima de é de , porque está acima do solo. Então, seja a altura do peso acima de e o comprimento da corda da roldana até o caminhão. Nós vamos determinar quando . Sendo assim, considerando que o ângulo em é um ângulo reto, em qualquer instante de tempo, vamos ter as seguintes relações no triângulo:
A partir dessas relações, nós vamos encontrar a derivada da altura em relação ao tempo.
Vamos lá!
Passo 2
Isolando na primeira relação, vamos ter:
Substituindo na segunda equação do passo , teremos:
Agora derivando ambos os lados da equação em relação a , usando a regra da cadeia, temos:
E isolando na equação:
Passo 3
Como conhecemos , falta apenas determinar no instante em que a altura . Da relação do triângulo que substituímos no passo , temos:
Tirando a raiz dos dois lados:
Substituindo esse valor na equação da variação da altura, com e , teremos:
Isso significa que a altura do peso no instante em que ele está a do solo, varia a uma taxa de aproximadamente .
Valeu, galera! Até a próxima! 😉