Use o Teorema de Stokes para calcular a integral do campo vetorial , onde é a curva dada pela interseção do cilindro com o plano , orientada no sentido anti-horário quando visto de cima.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma função vetorial e pediu pra gente calcular a integral dela sobre a superfície usando o Teorema de Stokes. Mas vamos por partes, primeiro vamos entender que superfície é essa. Ele nos disse que é dado pela interseção do cilindro com o plano , no gráfico isso fica assim:
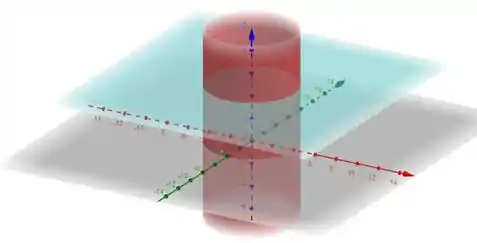
Repare que a interseção do cilindro em vermelho com o plano em azul claro é justamente a circunferência que aparece ali sombreada (guarda essa informação). Nós precisamos calcular a integral do campo vetorial e ele pediu pra gente fazer isso usando o Teorema de Stokes. Mas que Teorema é esse?
O Teorema de Stokes nos diz que a integral de linha do campo vetorial, em uma superfície fechada, simples e com orientação positiva, pode ser calculada através da relação:
Então, a gente transforma uma integral de linha em uma integral dupla de superfície. No nosso caso, é a circunferência que aparece ali em cima (da interseção entre o cilindro e o plano). Além disso, é o vetor normal à superfície e é o rotacional da função vetoria , que é calculado por:
Então, nós vamos calcular o rotacional da função, encontrar o vetor normal da superfície e aplicar na integral fazendo as mudanças de coordenadas necessárias.
Vamos lá!
Passo 2
Vamos começar definindo nossa superfície . Nós já vimos que a interseção entre o cilindro e o plano vai nos fornecer uma circunferência, mas que circunferência é essa? Ela vai ser dada pela borda do cilindro . Se nós pegarmos o disco do plano , vamos ter a função:
Onde é a nossa região .
Pra calcular o vetor normal a essa região, precisamos calcular o produto vetorial .
Então, vamos começar derivando a função em relação a :
Agora derivando em relação a :
Calculando o produto vetorial, vamos ter:
O determinante no dá:
Esse é o nosso vetor normal .
Passo 3
Agora vamos calcular o rotacional da função usando a fórmula:
Calculando as derivadas parciais das componentes , e vamos ter:
Substituindo na integral, junto com o vetor , temos:
Vamos calcular esse produto escalar no integrando:
Mas o enunciado disse que , então temos:
Passo 4
Lembra que a gente definiu lá no passo ? Ele é a nossa região de integração:
Como a gente sabe que ela é uma circunferência, o ângulo varia de a . E o raio é dado pela equação, . Logo:
Pra facilitar nossa vida na hora de integrar, vamos fazer uma mudança para coordenadas polares, onde:
Substituindo na integral, temos:
Integrando em relação a :
Aplicando os limites de integração:
Agora integrando em relação a , temos:
Aplicando os limites de integração em :
Prontinho, galera! Até a próxima! 😉