Seja
É dado que
- Determine
- Ache a área do triangulo limitado pelos eixos e pela reta tangente ao gráfico de no ponto .
Passo 1
- Pelo Teorema Fundamental do Cálculo, nós temos que se uma função continua é dada por
Então,
Ok, mas como eu aplico isso para resolver a letra a?
Repara que aqui queremos achar a derivada de uma função em , que é a .
E a é definida como uma integral, que tem como variável . Ou seja, podemos dizer que
Opa, isso é um indicativo que podemos resolver pelo Teorema Fundamental do Cálculo. Então vamos aplica-lo para achar
Passo 2
Antes de aplicar o Teorema Fundamental do Cálculo, repara em uma coisinha:
No problema o está no limite inferior e a constante no limite superior. E o para resolver pelo Teorema Fundamental do Cálculo, como no exemplo do Passo 1, teria que ser o contrario.

Mas fica tranquilo, que é só usar aquela propriedade de troca de limites esperta para inverter os limites, lembra?
A gente simplesmente inverte os limites da integração e coloca um sinal de menos na frente da integral. Então utilizando a propriedade fica assim:
Passo 3
Agora sim nós podemos aplicar nosso maravilhoso Teorema Fundamental do Cálculo. Bom, já que temos agora que:
E dado que a função é contínua no intervalo .
Então podemos aplicar o teorema nesse caso, chegando nisso aqui:
Passo 4
O que a questão pede é e não . Observe que é uma função. Quando queremos calcular o valor de uma função de em dado ponto, o que fazemos? Não é simplesmente substituir pelo valor da função naquele ponto?
Então é isso que vamos fazer!
Fazendo
Passo 5
b) Para acharmos essa área, primeiro temos que achar a reta tangente. E como que achamos a reta tangente? Vamos fazer igual quando fazíamos lá em derivadas:
Como ele pede para o ponto:
Para a nossa alegria, já temos o valor de que calculamos no passo anterior, que é igual a .
Agora vamos encontrar
Passo 6
Antes disso, vamos chamar a primitiva da integral de .
Ok, perceba que ele deu a seguinte expressão no enunciado:
Se a gente tivesse que calcular isso passo-a-passo, primeiro a gente encontraria a primitiva para depois substituir os limites de integração, assim:
Agora compare com a expressão de :
Percebe que a função de dentro da integral não mudou? Então a primitiva, , é a mesma.
A única coisa que mudou foi que o que aparecia no limite inferior da integral virou .
Então quando a gente substituir 1 na expressão, teremos,
Beleza, agora vamos montar a nossa equação:
Passo 7
Agora que já temos a equação da reta tangente, podemos traçar o gráfico para calcular a área:
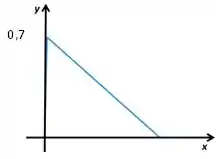
Temos uma região que corresponde a um triângulo retângulo. Já sabemos que a área de um triângulo é dada por:
A base é a distância do ponto onde a reta corta o eixo até o ponto . Por isso, basta descobrimos onde a reta corta o eixo . Ela corta o eixo quando , concorda?
Então basta substituirmos na equação da reta e acharmos o valor de correspondente, beleza?
Temos . Fazendo :
Já a altura será , que é o ponto onde a reta tangente corta o eixo . Portanto, a área pedida será:
Onde “u.a.” significa unidade de área.