Considere o sistema:
Faça o que se pede abaixo:
i. Determine os valores de a e b para que o sistema tenha uma única solução e calcule sua solução.
ii. Determine os valores de a e b para que o sistema tenha infinitas soluções e calcule suas soluções.
iii. Determine os valores de a e b para que o sistema não tenha soluções.
Passo 1
Precisamos analisar a existência de solução desse sisteminha.
Então vamos começar montando a matriz aumentada dele:
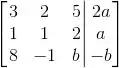
Só pra ficar mais fácil pra gente, vamos trocar a primeira linha com a segunda:
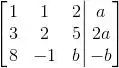
E agora vamos escalonar isso aí:
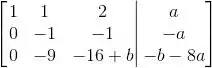
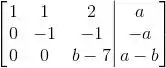
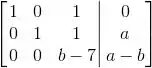
Passo 2
i. Para que o sistema tenha solução, todas as equações devem fazer sentido, né?
E mais do que isso, pra solução ser única, os valores das incógnitas devem ser bem definidos.
Então na última linha dessa matriz, teremos que ter:
Pois assim ficaremos com um número diferente de 0 igual a um outro número qualquer.
Aí as demais incógnitas vão ficar bem definidas também.
Pra ver isso é só continuar escalonando:
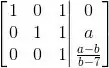
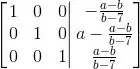
Então a solução única vai ser:
Passo 3
ii. Pra que o sistema tenha infinitas soluções, a última linha da matriz aumentada escalonada deve ser da forma:
Então:
Nesse caso a matriz vai ficar:

Pela primeira linha:
Pela segunda linha:
E as soluções vão ser do tipo:
Passo 4
iii. Pra não ter solução, as equações devem ser incoerentes.
Então na última linha da matriz aumentada escalonada, devemos ter:
um número diferente de 0
Pra isso ocorrer:
Resposta
i.
a qualquer
Solução:
ii.
Infinitas soluções da forma:
iii.