Considere o gráfico da derivada da função representado na figura abaixo:
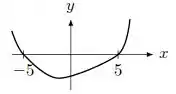
Pode-se afirmar que:
- O ponto é um mínimo local de .
- A função é crescente no intervalo .
- .
- A concavidade do gráfico de é para cima em .
Passo 1
Veja que temos o gráfico da derivada e não dá função, então fique atento. Nessa questão vamos ter que analisar alternativa por alternativa.
No ponto , temos a derivada negativa à esquerda e positiva à direita, então, pelo teste da primeira derivada, esse é de fato um ponto de mínimo. Logo, já temos a resposta. Vamos só ver se não há conflito com o resto do problema.
Passo 2
Veja que no intervalo a derivada é negativa, logo a função é decrescente e não crescente como sugerido na letra (b).
Passo 3
No ponto , a derivada está aumentando, logo a segunda derivada, que é a taxa de variação da primeira, é positiva e não negativa como sugerido na letra (c).
Passo 4
A derivada está diminuindo, logo a segunda derivada será negativa e a concavidade será para baixo e não para cima no intervalo sugerido na letra (d).
Resposta
Letra (a)