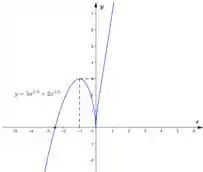
Questão 5 - Seja . Sabendo que e para todo , determine, caso existam:
(a) assíntotas horizontais e verticais do gráfico de ;
(b) intervalos onde é crescente e intervalos onde é decrescente;
(c) máximos e mínimos locais de ;
(d) intervalos onde o gráfico de é côncavo para cima e intervalos onde o gráfico de é côncavo para baixo;
(e) pontos de inflexão do gráfico de .
Utilizando os resultados dos itens anteriores, esboce o gráfico de .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão foi dada uma função em que
Além disso, vemos que a primeira derivada da é dada por
Já a segunda derivada de é
Ambas para diferente de .
A partir dessas informações, temos que encontrar as respostas para as perguntas dadas no enunciado.
Preparado? Vamos analisar item por item!
Bora lá! 😎
Passo 2
No item a) queremos calcular as assíntotas verticais e horizontais da função .
Começando pelas assíntotas verticais... elas são obtidas em pontos onde a função não é definida. Obtidos esses pontos, calculamos o limite de com tendendo a esse valor.
Se analisarmos a função , vemos que não há assíntotas verticais, pois é definida em todo o conjunto dos números reais!
Agora para as assíntotas horizontais... podemos obtê-las calculando o limite de quando tende ao infinito.
Se esse limite resultar em uma constante , a equação é a equação da assíntota.
Substituindo por temos que
Portando, também não há assíntotas horizontais em !
Tranquilo até aqui? 👀
Passo 3
No item b) queremos saber em qual intervalo a função é crescente e em qual intervalo a função é decrescente.
A função que nos diz qual é seu coeficiente angular é a função derivada. Se for positiva, a função é crescente... mas se for negativa, é decrescente.
No enunciado foi dito que é dada por
Vamos fazer uma análise dos sinais do numerador e do denominador para ver em quais momentos a função é positiva e em quais momentos a função é negativa.
Analisando o numerador durante o intervalo , ou seja, os números reais positivos, vemos que é positivo durante todo o tempo.
Agora se analisar no conjunto dos números reais negativos vemos que é menor que , exceto quando , portanto
Agora fazendo a mesma análise para o denominador . Como está em uma raiz cúbica, se for positivo será positivo, se for negativo também será negativo. Logo
Resumindo, temos que quando numerador e denominador tiverem os mesmos sinais, será positiva, caso o contrário, será negativa.

Portanto, a função é crescente no intervalo de e e decrescente no intervalo de .
Interessante, não é? 😁
Passo 4
Já no item c) queremos encontrar os máximos e mínimos da função .
Estes são obtidos a partir das derivadas de primeira e segunda ordem da função.
A primeira coisa que temos que fazer é igualar a . Com isso vamos obter possíveis valores para e esses valores são os pontos críticos de .
Vamos começar!
Multiplicando os dois lados por , temos
Isolando
Mas como não está definida em , vamos considerar esse ponto também.
Pela tabela que vimos anteriormente

Vemos que passa de positivo para negativo em e de negativo para positivo em .
Portanto, se lembrarmos que é a tangente de , podemos afirmar que é um ponto máximo da nossa função e em é um ponto mínimo de .
Entendeu? 😎

Passo 5
No item d) temos que obter os intervalos de concavidade da função .
Ou seja, em qual intervalo de a função tem concavidade voltada para baixo e em qual intervalo essa concavidade é voltada para cima?
Pra isso, vamos usar a segunda derivada de , se for positiva a concavidade de é para cima, mas se for negativa, a concavidade de é voltada para baixo.
Fazendo a mesma análise dos sinais no numerador e no denominador, vemos que no numerador o sinal resultando será positivo se , ou seja
Agora para ser negativo temos que ter
Logo, o numerador é negativo se for menor que .
Fazendo a mesma análise para o denominador , vemos que como está elevada a potência, para qualquer valor que escolhermos será positivo.
Construindo uma tabela similar à que fizemos no passo 3, temos que

Como não é definido em , dizemos que tem a concavidade voltada para baixo quando é negativa, no intervalo e a concavidade voltada para cima quando for positiva, ou seja, em
Sacou essa parte? 👍
Passo 6
Por fim, no item e) temos que obter os pontos de inflexão de e esboçar seu gráfico.
O ponto de inflexão acontece quando muda de sinal, na prática o ponto de inflexão é o ponto onde a função muda de concavidade.
Na tabela que acabamos de ver, o único ponto em que a função muda de sinal, é em .
Portanto, esse é o nosso único ponto de inflexão!
Já para esboçar o gráfico da função , vamos usar as informações que obtemos até agora, como concavidade, ponto de inflexão, pontos críticos, assíntotas, intervalos de crescimento...
Assim, obtemos algo parecido com
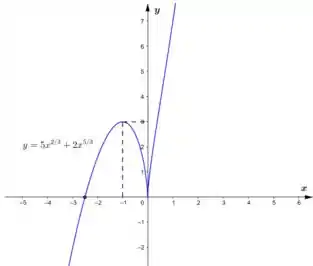
Bonitinho, não é? 😎
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta
a) Não há assíntotas verticais e horizontais.
b) é crescente no intervalo de e e decrescente no intervalo de .
c) é um ponto máximo e é um ponto mínimo.
d) Voltada para baixo no intervalo e voltada para cima no intervalo .
e) .