Seja , para . Qual dos seguintes pontos é ponto de mínimo local de ?
Passo 1
Bora lá galera. Olha só, pontos de máximo ou de mínimo são sempre pontos críticos. Portanto, pra achar todos os pontos críticos basta a gente derivar e igualar a zero, ok? Vamos lá, pela regra da cadeia, temos:
O arco cujo seno é é um daqueles arcos de bem definidos! Então tá na mão! Olhando a tabela abaixo e o círculo trigonométrico, vemos que:
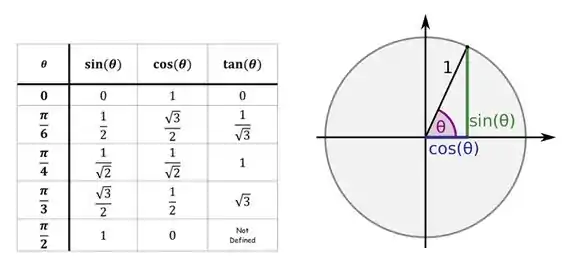
Os pontos críticos vão ser então:
Passo 2
Pra saber se um ponto é de máximo ou mínimo, a gente pode usar um recurso interessante com a segunda derivada. Veja bem:
- Se o ponto crítico (que é raiz de ) está dentro de um intervalo de crescimento de , então antes de , e depois de , . De tal forma que , e logo é um mínimo local.
- Se o ponto crítico (que é raiz de ) está dentro de um intervalo de decrescimento de , então antes de , e depois de , . De tal forma que , e logo é um máximo local.
Veja esse exemplo:
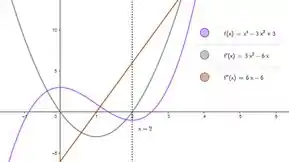
Veja que o ponto crítico se encontra num intervalo de decrescimento de , algo evidenciado pelo fato de a inclinação da reta tangente de em , isto é, , ser menor que zero. Logo é um máximo local. Veja também que o ponto crítico se encontra num invervalo de crescimento de , algo evidenciado pelo fato de a inclinação da reta tangente de em , isto é, , ser maior que zero. Logo é um mínimo local.
Passo 3
Deu pra ver então que vamos precisar da segunda derivada! Fazendo ela, pela regra da cadeia, temos:
Opa, como os pontos críticos são:
Vamos notar que:
São pontos de máximo local então:
Agora é só olhar nas respostas quais opções são possíveis de fazer pra escolhas de inteiros. Note que se
E prontinho! Fechamos a questão! A resposta vai ser a letra