Sejam e dadas por
Onde e são constantes reais positivas.
Prove que é o valor máximo de .
Passo 1
Para que seja um valor de máximo dessa mesma função devemos garantir que é positiva antes de , negativa depois desse valor e igual a em . Vamos derivar e fazer a análise de seu sinal:
Passo 2
Observando esse termo que chegamos na última linha reparamos que o sinal da derivada vai depender só do numerador, pois o denominador está elevado a uma potência par e, por isso, vai ter como valor sempre um número positivo. Esse termo de cima pode ser aberto em dois polinômios do primeiro grau cujas raízes podem ser calculadas por Bhaskara:
Então,
Dessa maneira, podemos fazer o quadro dos sinais para analisar se é de fato positiva antes e negativa depois de .
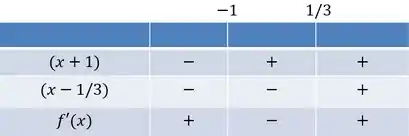
Realmente, é positiva antes de , negativa depois desse valor e igual a em .
Passo 3
Para garantir agora que esse é um máximo global e não só local temos que garantir que não tenha descontinuidades cujos limites explodam para e que seus valores quando sejam menores que .
Quanto às descontinuidades, ao observar a função, notaremos que não existe nenhuma, o domínio da função dorresponde aos números reais!
Agora, vamos calcular o valor de e os limites quando tem ou :
Enfim, como , tem o maior valor de !
Resposta
Ei, a resposta está no passo a passo :)