Calcule
Passo 1
Antes de tudo, vamos analisar com calma aqui rapidinho. Repare que varia desde até e essa expressão nada mais é do que a parte com positivo da circunferência .
No termo que vamos integrar, temos e . Já entendeu onde queremos chegar? Isso tudo indica que a boa aqui é usar coordenadas polares. Vamos fazer isso então!
Como já vimos, o Jacobiano dessa transformação é .
Passo 2
Para a gente não se confundir, vamos desenhar essa região de integração e descobrir os intervalos de e , ok? Como já falamos, varia desde até um arco de circunferência. Olhando para a integral, vemos que varia de até . Então temos:
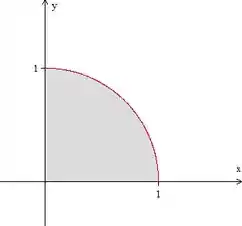
É isso aqui o que temos então. Agora ficou mais fácil de ver que e (o equivalente a de volta do círculo).
Passo 3
Vamos, então, montar a integral, substituindo os valores que atribuímos a e :
Esse vem do Jacobiano!
Passo 4
Vamos começar integrando em relação a :
Passo 5
Agora integramos em relação a . Para isso, vamos fazer a substituição: