Considere e a integral dada por
- Usando coordenadas polares calcule . Justifique.
Passo 1
Vamos começar entendo como é a região . Consegue perceber que temos duas circunferências?
Essa tem raio e centro em
Essa tem raio e centro em
A região vai ser a região interna a circunferência maior e externa a circunferência menor, conseguimos ver isso pela desigualdade das equações. Além disso, vamos ter e , então estamos pegando a parte do quadrante. O seu gráfico vai ficar
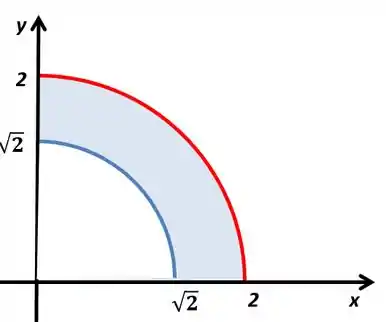
Passo 2
Usando as coordenadas polares vamos ter
Passo 3
Agora que já definimos a substituição que faremos, vamos analisar os intervalos de integração. Como já vimos, A região vai ser a parte entre os círculos, isso nos diz que vai do raio de um círculo até outro, ou seja,
Além disso, como temos o círculo apenas no primeiro quadrante o vai variar
Então
Passo 4
Vamos, então, montar a integral em coordenadas polares:
A integral vai ficar
Passo 5
Vamos resolver a integral
Pegamos sem o porque estamos considerando ele como uma constante, ou seja, basta multiplicar o resultado por ele depois.
Para isso basta fazermos
Substituindo na integral
Desubstituindo
Vamos ignorar essa constante porque temos a integral definida.
Passo 6
Voltando para