UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Prof° Aniura Milanés - Exercícios de EDB - 2021.1, Questão 23a
Para cada uma das funções abaixo, definidas no intervalo , obtenha sua série de Fourier e esboce seu gráfico no intervalo .
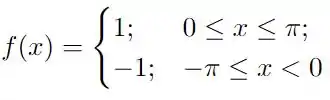
Passo 1
Eaew, tudo certinho?
Precisamos calcular a série de Fourier da seguinte função
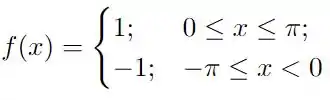
para isso, iremos calcular os coeficientes de Fourier
e, substituí-los na expressão
Por último precisamos fazer o plot do gráfico desta série! Vamos começar calculando os coeficientes não-nulos! Vem comigo!
Passo 2
Temos a seguinte função
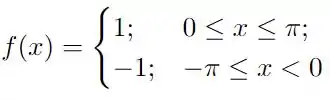
essa função é simplesmente no intervalo , e para . Portanto, essa é uma função de paridade ímpar de forma que só precisamos calcular os coeficientes do seno, dados por
as integrais podem ser obtidas diretamente como
Avaliando os limites, temos que
e, a segunda se torna
e, o nosso coeficiente não nulo é simplesmente
Vamos escrever a série e plotar o seu gráfico! Saca só!
Passo 3
Temos que para , números pares, , portanto . Também temos que se , números ímpares, , e temos simplesmente
Nossa série pode ser escrita como
o gráfico pode ser obtido como
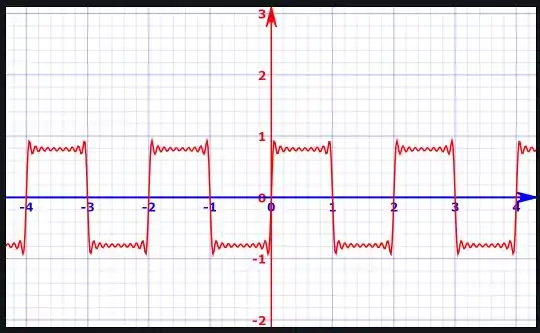
O comportamento se repete por toda a extensão do intervalo pedido! A questão foi isso, te vejo na próxima! Tchau Tchau!