UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 26g
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
Fala pessoal, tudo tranquilo por aí?
Nessa questão recebemos uma função definida por partes da seguinte forma:
A partir disso, precisamos determinar a série de Fourier de apenas em senos.
Pra escrevermos a série de Fourier de uma função apenas em senos, é necessário que a função seja ímpar e periódica.
Porém, nossa só está definida no intervalo , e por isso não é nem ímpar nem periódica.
Logo, a primeira coisa que vamos fazer é expandir a definição de de modo que ela se torne ímpar e periódica.
Depois que fizermos isso, podemos usar a teoria normal da série de Fourier pra funções ímpares e periódicas pra encontrar a sua expansão:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!!
Passo 2
Bom, pra começar, vamos expandir a definição de .
No intervalo , nossa é dada por:
E, a função seno é ímpar. Logo, já podemos definir no intervalo , como:
Massa! Já no intervalo , temos que:
Logo, para a função ser ímpar, podemos definir no intervalo , como:
Assim, temos:
E, para que seja periódica, podemos dizer que a partir dessa definição em , é periódica de período .
(Isso é um truque bem legal e importante de ter em mente no contexto das séries de Fourier. Não precisamos definir pra cada intervalozinho, pois pra ela ser periódica essa definição fica mudando.)
Massa!
Agora vamos desenhar o gráfico dessa função no intervalo :
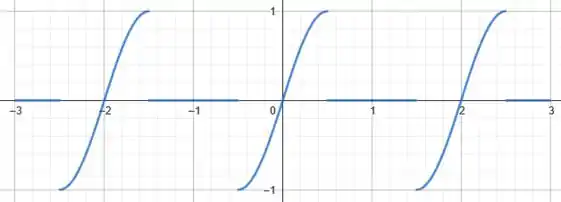
(consideramos sem perda de generalização).
Show de bola! Vamos pra série de Fourier efetivamente!!
Passo 3
Agora vamos determinar efetivamente a nossa série de Fourier. Para isso, precisamos determinar :
Como nossa é definida por partes, vamos abrir a integral acima nos dois intervalos considerados:
Perfeito! Então precisamos resolver a integral acima.
Para isso podemos usar uma relação trigonométrica muito importante, que é a da transformação de produto em soma:
Aplicando no nosso problema, temos que:
Daí, temos:
Logo:
Daí, substituindo na integral, vamos ter:
Reduzimos ainda mais o nosso probleminha, agora precisamos calcular as duas integrais acima.
Já para a outra integral:
Juntando os dois resultados, vem que:
Usando que:
Analogamente:
Substituindo em :
Logo:
Perfeito!
Se for par, temos:
Se for ímpar, temos:
Logo, podemos escrever:
Muito bom!!
Passo 4
Agora que já calculamos , podemos finalmente escrever a série de Fourier de :
Prontinho pessoal! Matamos mais uma questão!
Vocês curtiram? Muito obrigado pela atenção de vocês 😊