UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 26a
Obtenha a série de Fourier em senos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
Fala aí galera, tudo bem por aí?
Nessa questão recebemos a função:
E, precisamos obter a série de Fourier em senos dessa função.
Puts!!! A função cosseno é uma função par, mas pra obtermos uma série de Fourier apenas em senos precisamos estar tratando de uma função ímpar. Será que o enunciado tá errado?
Nãooooo hahaha... é um tipo de probleminha mais complicado mesmo, mas tem uns truques bem legais que vamos aprender, então vem comigo!
A ideia principal pra conseguir escrever uma série de Fourier apenas de senos para uma função qualquer, é que podemos estender o gráfico da função dada, definindo ela por partes, de modo a forçá-la a ser ímpar.
Depois disso, podemos seguir a ideia normal de série de Fourier de funções ímpares. Temos que:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!!
Passo 2
Bom, a primeira etapa é construirmos o gráfico da nossa função no intervalo de modo que ela seja ímpar e periódica.
No contexto da série de Fourier, temos que o período da função vale:
Assim, pra determinarmos , e consequentemente , precisamos antes determinar o período da função.
“Ah, fácil. O período do cosseno é
Muita calma nessa hora hahaha, de fato o período da função cosseno é , mas isso é quando ela está definida nos reais. Aqui, temos que foi definida apenas no intervalo .
Então, vamos definir de modo que ela realmente seja ímpar.
Vamos dizer que:
Com período, a princípio de . Pode ser que o período seja menor que , caso a curva para fique igual à curva para .
Sei que isso é um truque bem truquento, mas é a chave pra resolver esse tipo de exercício. Pois, definindo dessa forma, conseguimos fazer ser válido:
Logo, tornamos ímpar 😊.
Daí, podemos traçar o seu gráfico. Primeiro vamos esboçá-lo no intervalo .
Vamos ter:
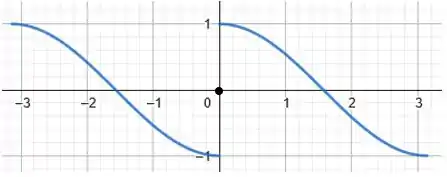
Olha que legal, quando redefinimos dessa forma encontramos que o seu período na verdade vale .
Assim:
Massa! Daí, pra traçar o gráfico no intervalo basta repetirmos essa figura do gráfico acima, a esquerda de e a direita de . Vamos ter:
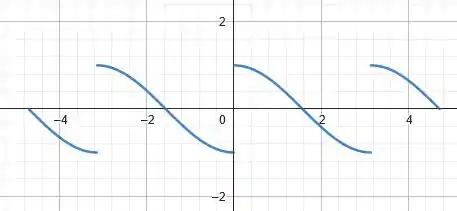
Prontinho! A primeira parte já foi 😊
Passo 3
Bom, como vimos no passo anterior, conseguimos definir como:
Mas, logo após vimos que o seu período vale . Então, poderíamos simplificar essa definição escrevendo:
com período .
“Ué, essa não é a mesma definição dada no enunciado?”
Mais ou menos gente, a grande diferença é que ampliamos o domínio da função pra todos os reais afirmando que o período dela é .
Além disso, precisávamos ter definido daquela forma mais elaborada pra forçar a função ser ímpar. O que aconteceu é que, no caso da função cosseno, ocorre uma “coincidência” da definição que usamos pra já se encaixar com a definição de .
Isso ocorre porque a curva de no intervalo é simétrica com relação à bissetriz do quadrante.
Beleza?!
Massa! Pra os coeficientes da expansão de em série de Fourier, precisamos fazer:
Como vimos , vamos ter:
Pra resolver essa integral, podemos usar a transformação trigonométrica de produto em soma. Basicamente, vale que:
Daí, temos:
Então:
Então:
Logo:
Perfeito! Vamos resolver essa integral!
Passo 4
Temos:
Substituindo os limites de integração, e lembrando que, se é impar, então:
E e são ímpares.
Logo:
Logo:
Aee! Conseguimos encontrar os coeficientes . Logo:
Onde:
Ufaaaa! Deu muito trabalho mas conseguimos encontrar a série de Fourier de . Obrigado pela atenção pessoal 😊
Resposta
Onde: