UFMG, Sem Campus, Equações Diferenciais B, Listas de EDB - Profª Aniura Milanés - Exercícios de EDB - 2021.1, Questão 27b
Obtenha a série de Fourier em cossenos de cada uma das funções a seguir. Você pode utilizar a applet da Sagemath disponibilizada no Moodle. Em cada caso, esboce seu gráfico no intervalo
Passo 1
E aí gente, tudo bem com vocês?
Nessa questão recebemos a função:
E, precisamos determinar a sua série de Fourier apenas em cossenos.
Sempre que queremos obter uma série de Fourier apenas em cossenos, precisamos que a função esteja definida como uma função par e periódica.
O problema é que, a função , quando definida nos reais, não é nem par nem periódica...
Nessas situações precisamos expandir o intervalo de definição de (observa que nesse problema ela foi definida apenas em ) de modo a torná-la par e periódica.
Depois disso, podemos seguir a ideia normal de série de Fourier de funções pares. Temos que:
onde:
Tranquilo até aqui? Vem comigo que vai ficar ainda mais claro!!
Passo 2
Bom, pra começar precisamos ampliar a definição de para torná-la par e periódica.
Para que ela seja par, precisa ser verdade que:
Se está nesse intervalo, . Assim, vamos definir no intervalo . Daí, na relação acima, onde tiver vamos trocar por :
Logo, podemos escrever a definição de como:
com periódica de período .
Isso significa que pra desenhar a curva de à esquerda e à direita de e , respectivamente, basta “colar” a mesa curva que aparece no intervalo . Assim, conseguimos de um jeito simples expandir a definição da nossa função pra todos os reais, e ainda forçando ela a ser ímpar e periódica. Sacaram?
Vamos então desenhar o seu gráfico no intervalo :
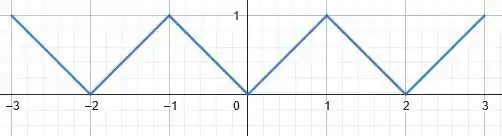
Show de bola! Vamos pra próxima parte agora 😊
Passo 3
Agora precisamos calcular efetivamente a série de Fourier de . Para isso precisamos calcular os coeficientes :
Pra calcular essa integral, precisamos usar o método de integração por partes. Dando uma rápida revisada, ele diz que:
Assim, fazendo:
Temos:
Como , temos que:
Logo:
Daí:
- Se é par:
- Se é ímpar:
Assim, podemos escrever que:
onde trocamos por para pegarmos apenas valores ímpares.
Ou seja:
Porém, aqui ainda temos um probleminha muito sutil...Conseguem ver qual é?
Passo 4
Quando resolvemos a integral que define , estávamos resolvendo para todos os possíveis valores de , inclusive . Mas, durante a resolução, em vários momentos escrevemos frações com no denominador, e se substituíssemos por 0, teríamos um absurdo matemático.
Por isso, precisamos calcular separadamente, a partir da definição de , colocando .
Se liga só:
Excelente!!
Daí, podemos escrever a série de Fourier como:
Aeee! Terminamos!
Até a próxima pessoal 😉