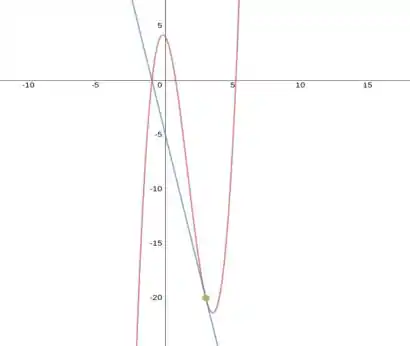
Escreva a equação da reta tangente à curva no ponto de abcissa .
Passo 1
A equação de uma reta é:
Aonde esse é o nosso coeficiente angular da reta e ele será justamente a derivada da curva naquele ponto, ou seja:
Além disso, sabemos que é uma função de , . Sendo assim . Então a equação geral da reta tangente é:
Só que queremos determinar a reta tangente no ponto , então:
Queremos então:
Passo 2
Vamos descobrir para isso basta substituir na equação
Certo, já dá para substituir alguma coisa:
Passo 3
Falta agora determinar . Para tal, derivamos nossa função :
Assim no ponto
Pronto! Já temos nossa reta:
Entao:
Olhe só que coisa linda:
Resposta
Exercícios de Livros Relacionados
Quantas retas tangentes à curva y = x / ( x + 1 ) passam pelo ponto ( 1 ,2 ) ? Em quais pontos essas retas tangentes tocam a curva?
Se G x = 4 x 2 - x 3 , encontre G ' ( a ) e use-o para encontrar equações das retas tangentes à curva y = 4 x 2 - x 3 nos pontos ( 2 ,8 ) e ( 3,9 ) .Ilustre a parte (a) traçando a curva e as retas tan
Encontre uma equação da reta tangente à curva y = 2 1 + e - x no ponto 0,1 .Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Encontre a equação da reta tangente à curva no ponto dado y = x - 1 x - 2,( 3,2 )
Esboce o gráfico de uma função f para a qual f 0 = 0 ,f ' 0 = 3,f ' 1 = 0ef ' 2 = - 1