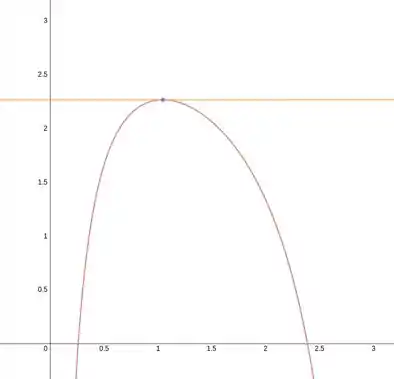
Sendo:
Encontre as equações para:
- A tangente à curva em .
- A tangente horizontal à curva em .
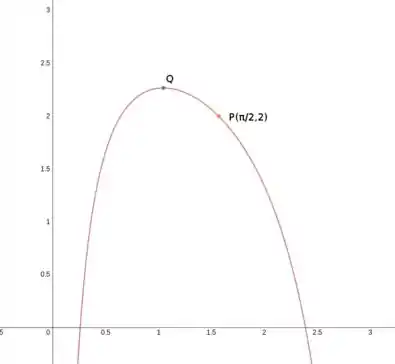
Passo 1
Primeiro temos que lembrar que equação geral da reta tangente é:
é um ponto em na curva. Então, agora o que temos que saber para achar a reta tangente é a nossa derivada para depois substituir o nosso na equação.
Vamos lá!
Passo 2
Então vamos derivar nossa função:
Como
E
A nossa derivada fica assim:
Passo 3
Pronto! Achamos a derivada, então vamos resolver a letra
a)
Repara que o enunciado forneceu qual que ele quer! No ponto . Então vamos substituir na fórmula
Então, galerinha, antes de começar a calcular só relembrando: csc e
Agora vamos lá! Calculando temos
Agora vamos para derivada ,
Pronto! Já podemos substituir esses valores na fórmula. A nossa reta fica assim:
Então a equação da reta tangente à curva em é:
Olhe como fica:
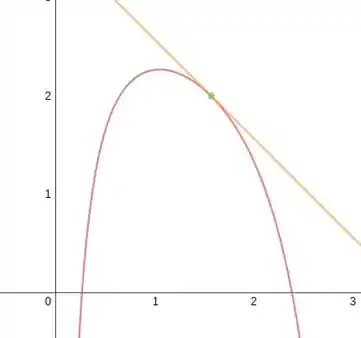
Passo 4
Agora a letra . Pode parecer complicado aqui o fato de você não sabe as coordenadas do ponto Q. Para não confundir, vamos chamar aqui no de , pois queremos a tangente neste ponto , ok?
Mas neste caso, o pulo do gato está no enunciado ter dito que a tangente nesse ponto é horizontal. Se a tangente é horizontal, o coeficiente dela é zero! Em outras palavras,
Então para achar quem é meu , eu preciso saber qual ponto minha derivada é zero,
O cosseno é igual em:
Existem muitos outros pontos onde o cosseno é igual a ½, mas este é o ponto que queremos, pois, olhando no gráfico do enunciado:
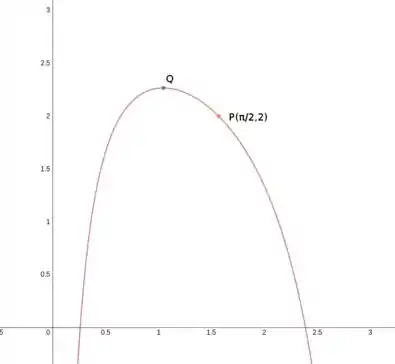
Vemos que a coordena de está entre e . O único ponto onde o cosseno é ½ entre esses valores é .
Passo 5
Pronto! Já temos o ponto . Agora é substituir na fórmula:
Vamos voltar a nossa equação original e descobrir :
Então:
Lembra que a nossa derivada no ponto é igual a zero?
substituir esses valores na fórmula. A nossa reta fica assim:
Então a equação da reta tangente à curva em é: