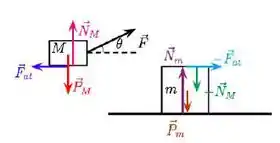
Uma caixa de massa está sobre outra caixa, de massa , tal que . Uma pessoa tenta arrastar as caixas, puxando a de cima com uma força de módulo F, que faz um ângulo com a horizontal, conforme a figura abaixo.
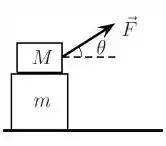
Sabe-se que o atrito entre a caixa de baixo e o chão pode ser desprezado e que o coeficiente de atrito estático entre as duas caixas é . Observa-se que o sistema composto pelas duas caixas se desloca em conjunto.
(a) Isole as caixas e faça um diagrama indicando as forças que atuam sobre cada uma
delas.
(b) Qual a aceleração das caixas?
(c) Qual o menor valor que pode ter para que o sistema continue a se movimentar em
conjunto?
Passo 1
- Traçando os diagramas de corpo livre:
- Calcularemos a aceleração das caixas (eixo x):
- Cálculo de :
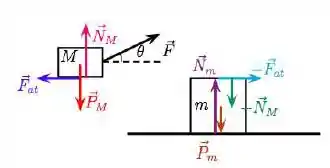
Sobre a caixa de cima atuam a força , a força peso , a normal que a caixa debaixo exerce sobre ela e a força de atrito que a caixa debaixo exerce . No bloco de baixo, além das duas reações às forças que ela exerce sobre a de cima ), atuam a força peso e a normal que o chão exerce .
Passo 2
Analisando a caixa 1:
Eixo x:
Analisando a caixa 2:
Eixo x:
Substituindo (2) em (1), temos:
Utilizando a relação entre as massas dada no enunciado e sabendo que as acelerações são iguais pois os blocos se movimentam juntos, teremos:
Passo 3
Tendo encontrado a aceleração no ítem anterior, podemos calcular a como:
Sabendo que a força de atrito máxima é dada por:
Podemos dizer que:
Calculando
Fazendo o equilíbrio do bloco de cima:
Eixo y:
Logo, o menor valor de será: