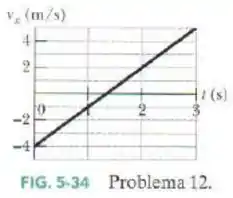
Duas forças horizontais e agem sobre um disco de que desliza sem atrito sobre o gelo, no qual foi desenhado um sistema de coordenadas . A força aponta no sentido positivo do eixo e tem módulo de . A força tem um módulo de . A Fig. 5-34 mostra a componente da velocidade do disco em função do tempo . Qual é o ângulo entre as orientações constantes das forças e ?
Passo 1
Fala pessoal, vem comigo pra mais um?
Vamos fazer um desenho para entendermos o que tá se passando.
A Força está na direção do eixo .
Já a força está numa posição qualquer, então vamos colocar com um ângulo qualquer da :
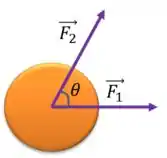
A ideia é que com o gráfico da velocidade sobre o tempo, conseguimos a aceleração no eixo . Feito isso, podemos aplicar a Segunda Lei de Newton e descobrir a força resultante na direção :
Por fim, podemos relacionar a força resultante com a soma na horizontal de e . E aqui é o seguinte a força horizontal nós temos e também, só vai faltar aí é decompor essa força inclinada pra horizontal, e é aí que o ângulo vai aparecer então fiquem ligados pois é esse ângulo que a gente quer!
Passo 2
Vamos usar o gráfico dado para obter informações.
Observando bem ele, conseguimos ver que o movimento no eixo se trata de um MUV, porque a velocidade varia uniformemente (reta).
A aceleração é a variação da velocidade:
Logo, basta pegar quaisquer dois pontos do gráfico e calcular esse .
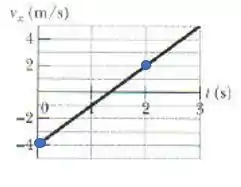
Aqui vou escolher o ponto inicial:
e
E o ponto final:
e
Você poderia ter escolhido outro ponto também se quisesse o ideal é escolher um ponto fácil de trabalhar, assim:
Com a aceleração bora pra força em .
Passo 3
Agora nós temos: a aceleração no eixo e a massa do disco, portanto, podemos usar da segunda lei de Newton para achar a força resultante no eixo :
Com e a aceleração encontrada temos:
Passo 4
Agora, para achar o ângulo vamos fazer o somatório de forças na horizontal.
Bom, mas já está na horizontal, porém não...
Logo, temos que pegar sua componente horizontal:
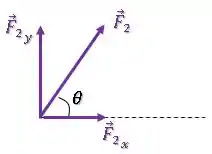
Aqui por trigonometria vamos decompor essa força fazendo a seguinte relação:
E encontramos alguma relação com o ângulo que queremos, vamos dar um jeito de isolar ele jajá.
Passo 5
Aplicando a segunda lei de Newton temos que o somatório das forças horizontais é:
Beleza, conhecemos todo mundo aqui mas antes vamos isolar o cosseno do ângulo pra encontrar o ângulo depois!
Vamos substituir os valores calculados e dados do enunciado.
Substituindo na equação temos:
Agora pra encontrar o ângulo vamos fazer a trigonométrica inversa, mas o que é isso? Pro cosseno a inversa é conhecida como arcocosseno, e a gente lê como se fosse “O arco cujo cosseno é ”. E aí você inverte, tira o do cosseno e coloca no número que você calculou.
Talvez na sua calculadora essa função apareça como , mas não esquenta é a mesma função só vai ficar assim:
Encontramos o nosso ângulo, vamos praticar mais juntos??