Uma força de módulo é exercida no lado esquerdo da face de dois blocos que estão colocados lado-à-lado em uma superfície sem atrito, com as duas faces se tocando. A inércia do bloco da direita é e a do bloco da esquerda é .
a) Desenhe o diagrama de corpo livre dos blocos e calcule o módulo da aceleração de cada bloco. b) Qual o módulo e sentido da força de contato que o bloco da esquerda exerce no bloco da direita?
c) Qual o módulo e sentido da força de contato que o bloco da direita exerce no bloco da esquerda?
d) Como suas respostas se alteram nas partes a), b) e c) se a posição dos dois blocos é invertida?
Passo 1
De todas as situações possíveis que podemos imaginar o problema, acredito que a que a que ele queira que a gente imagine seja
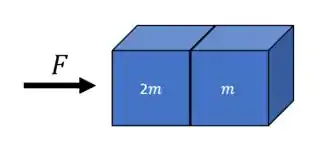
E aí fica de exercício pra vocês amiguinho ... pensar em todas as situações possíveis e como nossos queridos professores também tem problemas para serem claros nos enunciados hahaha.
Queremos resolver nosso problema ao ponto de que newton tenha esperanças que iremos nos formar um dia haha.
Passo 2
(a) Da ilustração do passo 1, vamos começar pelo que o item nos pede, o diagrama de corpo livre. Quais são as forças que estão atuando em nosso problema?
Como já desenhamos, temos a força descrita no enunciado que é aplicada a esquerda dos nossos blocos.
Devido o contato, temos que o bloco da esquerda também aplica uma força no bloco da direita e pela 3ª Lei de Newton temos que toda ação tem uma reação, assim o bloco da esquerda também aplica uma força no bloco da direita.
Por ultimo mais não mesmo importante temos as forças pesos e normais do problema. Desta forma nosso diagrama é dado por
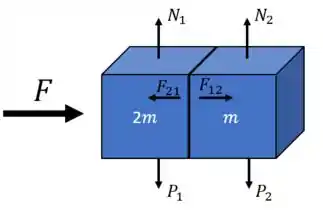
Agora tomando que os dois blocos estão “grudados”, temos que a aceleração é o vínculo do problema, ou seja, ambos os blocos possuem a mesma aceleração. Desta forma
O que nos leva a concluir que o módulo da aceleração de cada bloco será
Passo 3
(b) O bloco da direita empurra do bloco da esquerda. Já sabemos que ambos os blocos possuem como vínculo a aceleração, logo possuem a mesma direção e sentido. Assim temos que a força que o bloco da esquerda exerce no bloco da direita será
Como sabemos que a aceleração, então
Passo 4
(c) Como diria Newton, “que a força esteja com você” ... talvez ele não diria isso, mas ainda bem que ele formulou a terceira lei, no informando que toda ação tem uma reação de mesmo módulo, direção, mas sentido oposto. Assim temos que
em módulo.
Passo 5
(d) Por todos nossos processos em construir nossas soluções, percebemos que tudo se manteria da mesma forma caso os blocos se invertessem de ordem.
Resposta
- Nadica de nada